

分析 (1)①由DE∥BC,得到△ADH∽△ABG和△AHE∽△AGC,即可得到结论;②易证△DEN∽△AEM,△OND∽△OMB,则依据相似三角形的对应边的比相等,可以证得$\frac{CG}{BG}$=$\frac{BG}{GC}$,得到BG=CG,即点G是BC的中点;
(2)①连接AC,BD,两线交于点O1.②在矩形ABCD外任取一点E,连接EA,EB,分别交DC于点G,H③连接BG,AH,两线交于点O2.④作直线EO2,交AB于点M.⑤作直线MO1.直线MO1就是矩形ABCD的一条对称轴.
解答 (1)证明:①∵DE∥BC,
∴△ADH∽△ABG,
∴$\frac{DH}{BG}$=$\frac{AH}{AG}$,
同理$\frac{HE}{GC}$=$\frac{AH}{AG}$,
∴$\frac{DH}{BG}$=$\frac{HE}{GC}$;
②∵DE∥BC,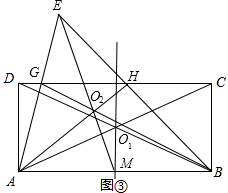
∴△FDH∽△FCG,
∴$\frac{DH}{CG}$=$\frac{FH}{FG}$,同理$\frac{EH}{GB}$=$\frac{FH}{FG}$,
∴$\frac{DH}{CG}$=$\frac{HE}{GB}$,
∴$\frac{DH}{HE}$=$\frac{CG}{BG}$,
由(1)得$\frac{DH}{HE}$=$\frac{BG}{GC}$,
∴$\frac{CG}{BG}$=$\frac{BG}{GC}$,
∴BG=CG,即点G是BC的中点;
(2)如图③所示,直线MO1即为所求.
点评 本题考查了相似三角形的判定与性质,正确根据相似三角形的对应边的比相等,通过等量代换得到$\frac{CG}{BG}$=$\frac{BG}{GC}$是做题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
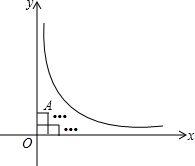 如图,在曲线y=$\frac{3}{x}$(x>0)与两坐标轴之间的区域A内,最多可以水平排放边长为$\frac{1}{2}$的正方形35个.
如图,在曲线y=$\frac{3}{x}$(x>0)与两坐标轴之间的区域A内,最多可以水平排放边长为$\frac{1}{2}$的正方形35个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com