
分析 (1)根据蔬菜的单价乘以蔬菜的数量,可得函数关系式;
(2)根据利润等于出售价格减去收购成本、减去每天的费用,可得方程,根据解方程,可得答案;
(3)根据利润等于出售价格减去收购成本、减去每天的费用,可得二次函数,根据二次函数的性质,可得答案.
解答 解:(1)由题意得y与x之间的函数关系式为y=(10+0.5x)(2000-6x)
=-3x2+940x+20000(1≤x≤110)
(2)由题意得:-3x2+940x+20000-10×2000-340x=22500
解方程得:x1=50;x2=150(不合题意,舍去)
经销商想获得利润2250元需将这批蔬菜存放50天后出售.…(6分)
(3)设最大利润为W,由题意得W=-3x2+940x+20000-10×2000-340x
w=-3(x-100)2+30000,
∴当x=100时,W最大=30000
100天<110天
∴存放100天后出售这批蔬菜可获得最大利润30000元
点评 本题考查了二次函数的应用,利用利润等于出售价格减去收购成本、减去每天的费用得出二次函数是解题关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 4月份商场的商品销售总额是75万元 | |
| B. | 1月份商场服装部的销售额是22万元 | |
| C. | 5月份商场服装部的销售额比4月份减少了 | |
| D. | 3月份商场服装部的销售额比2月份减少了 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
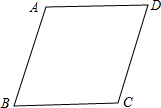 如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是16,则菱形ABCD的面积是$\frac{128\sqrt{3}}{9}$.
如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是16,则菱形ABCD的面积是$\frac{128\sqrt{3}}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知⊙O的直径AB=6,直线AC与⊙O相切于点A,线段AC=8,CB与⊙O相交于点M,⊙O的切线MP与AC相交于点P.
已知⊙O的直径AB=6,直线AC与⊙O相切于点A,线段AC=8,CB与⊙O相交于点M,⊙O的切线MP与AC相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com