
【题目】已知∠AOB为锐角,如图(1).
(1)若OM平分∠AOC,ON平分∠BOD,∠MON=32°,∠COD=10°,如图(2)所示,求∠AOB的度数.
(2)若OM,OD,OC,ON是∠AOB的五等分线,如图(3)所示,以射线OA,OM,OD,OC,ON,OB为始边的所有角的和为980°,求∠AOB的度数. 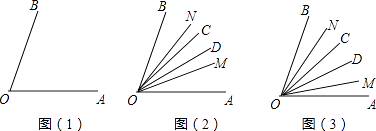
【答案】
(1)解:∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=∠COM,
同理:∠BON=∠DON,
∵∠MON=32°,∠COD=10°,∠MON=∠CON+∠DON﹣∠COD,
∴32°=∠COM+∠DON﹣10°,
∴∠COM+∠DON=42°,
∴∠AOM+∠BON=42°,
∵∠AOB=∠AOM+∠BON+∠MON,
∴∠AOB=42°+32°=74°
(2)解:设∠AOB被五等分的每个角为x°,则∠AOB=5x°,
以射线OA为始边的所有角的度数为x°+2x°+3x°+4x°+5x°=15x°,
以射线OM,OD,OC,ON,OB为始边的所有角的度数分别为11x°,9x°,9x°11x°,15x°,
由题意得15x+11x+9x+9x+11x+15x=980,
解得x=14.
故∠AOB=5×14°=70°
【解析】(1)根据角平分线的定义容易得到,∠MON=∠CON+∠DON﹣∠COD,根据已知条件求得∠COM+∠DON=42°,即可求得∠AOM+∠BON=42°,从而求得∠AOB=∠AOM+∠BON+∠MON=74.(2)设∠AOB被五等分的每个角为x°,则∠AOB=5x°,分别表示出以射线OA、OM、OD、OC、ON、OB为始边的所有角的度数,根据题意列出关于x的方程,解方程求得x的值,即可求得∠AOB的度数.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对角的运算的理解,了解角之间可以进行加减运算;一个角可以用其他角的和或差来表示.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】一件产品原来每件的成本是1000元,由于连续两次降低成本,现在的成本是810元,则平均每次降低成本( )
A. 8.5%B. 9%C. 9.5%D. 10%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE. 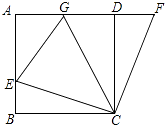
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组数中,以a、b、c为边长的三角形不是直角三角形的是( )
A.a=3,b=4,c=5
B.a=5,b=12,c=13
C.a=1,b=2,c= ![]()
D.a= ![]() ,b=2,c=3
,b=2,c=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下 ![]() 不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得 ![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)若(1,b)是“相伴数对”,求b的值;
(2)写出一个“相伴数对”(a,b),其中a≠0,且a≠1;
(3)若(m,n)是“相伴数对”,求代数式m﹣ ![]() ﹣[4m﹣2(3n﹣1)]的值.
﹣[4m﹣2(3n﹣1)]的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com