
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE. 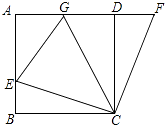
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
【答案】
(1)证明:在正方形ABCD中,
∵ 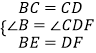 ,
,
∴△CBE≌△CDF(SAS).
∴CE=CF.
(2)解:GE=BE+GD成立.
理由是:∵由(1)得:△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,∴∠GCF=∠GCE=45°.
∵ 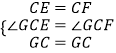 ,
,
∴△ECG≌△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
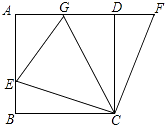
【解析】(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF.(2)由(1)得,CE=CF,∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④ ![]() 其中正确的有( )
其中正确的有( )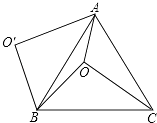
A.①②
B.①②③
C.①②④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论: ①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ ![]() .
.
其中正确的序号是(把你认为正确的都填上).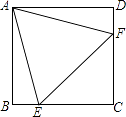
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n满足等式(m﹣8)2+2|n﹣m+5|=0.
(1)求m,n的值;
(2)已知线段AB=m,在直线AB上取一点P,恰好使AP=nPB,点Q为PB的中点,求线段AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB为锐角,如图(1).
(1)若OM平分∠AOC,ON平分∠BOD,∠MON=32°,∠COD=10°,如图(2)所示,求∠AOB的度数.
(2)若OM,OD,OC,ON是∠AOB的五等分线,如图(3)所示,以射线OA,OM,OD,OC,ON,OB为始边的所有角的和为980°,求∠AOB的度数. 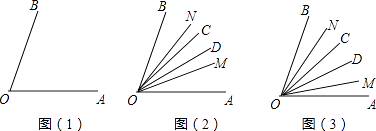
查看答案和解析>>
科目:初中数学 来源: 题型:
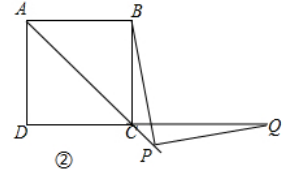
【题目】如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q. 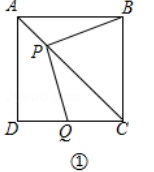
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com