
【题目】如图,在Rt△ABC中,∠C=90°,AC=-6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将ΔCEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )
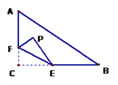
A. 1.6 B. 1.2 C. 1 D. 0.8
科目:初中数学 来源: 题型:
【题目】根据阳泉市教育局3月份通知,从2016年中考起,九年级学生信息技术考试成绩统计入中考总分,我县某中学为了提高八年级学生学习信息技术的积极性,组织了“信息技术技能竞赛”活动,八年级甲、乙两班根据初赛成绩,各选出5名选手参加复赛,这些选手的复赛成绩(满分为100分)如图所示:
(1)根据统计图填写下表:
班级 平均数(分) 众数(分) 方差
甲班 85 85
乙班 160
(2)根据上表可知,两个班选手成绩较稳定的是 ;

(3)选手小明说:“这次竞赛我得了80分,在我们班选手中成绩排名属下游!(后两名)”观察统计图,求出两班选手成绩的中位数,说明小明是哪个班的学生?
(4)学校要给其中一个班发集体优胜奖,你认为发给哪个班合适?请综合考评,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好的保护美丽图画的邛海湿地,西昌市污水处理厂决定先购买A、B两型污水处理设备共20台,对邛海湿地周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
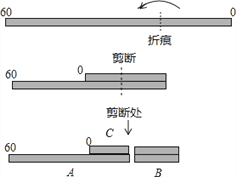
A. 20 B. 25 C. 30 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长为1,宽为a的矩形纸片(![]() ),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为_________.
),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为_________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为1、宽为![]() 的矩形纸片按如图①所示的方式折叠一下,剪下一个边长等于矩形宽度的正方形,称为第一次操作;再把剩下的矩形按如图②所示的方式折叠一下,剪下一个边长等于此时矩形宽度的正方形,称为第二次操作;如此反复操作下去……若在第
的矩形纸片按如图①所示的方式折叠一下,剪下一个边长等于矩形宽度的正方形,称为第一次操作;再把剩下的矩形按如图②所示的方式折叠一下,剪下一个边长等于此时矩形宽度的正方形,称为第二次操作;如此反复操作下去……若在第![]() 次操作后,剩下的矩形为正方形.则操作终止.当
次操作后,剩下的矩形为正方形.则操作终止.当![]() 时,
时, ![]() 的值为 _______.
的值为 _______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性。
结论:(1) ;
(2) ;
(3) ;
(4) ;
选择结论: ,说明理由:
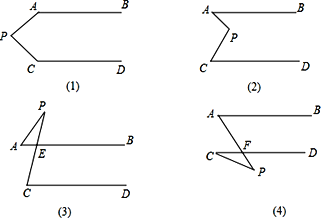
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com