
【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上的一点,且AC平分∠PAE,过C作CD⊥PA于点D.
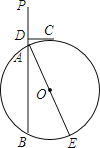
(1)求证:CD为⊙O的切线.
(2)若DC+DA=6,AE=26,求AB的长.
【答案】(1)见解析;(2)AB=24.
【解析】
试题分析:(1)连接OC,根据OA=OC推出∠OCA=∠OAC,根据角平分线得出∠OCA=∠OAC=∠CAP,推出OC∥AP,得出OC⊥CD,根据切线的判定推出即可;
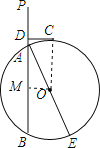
(2)过O作OM⊥AB于M,得出矩形OMDC,推出OM=CD,OC=AM+AD,求出AM=13﹣DA,利用勾股定理求出AD的长,即可求出AM的长,从而求出AB的长.
(1)证明:连接OC.
∵OC=OA,
∴∠OAC=∠OCA.
∵AC平分∠PAE,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴AD∥OC.
∵CD⊥PA,
∴∠ADC=∠OCD=90°,
即 CD⊥OC,点C在⊙O上,
∴CD是⊙O的切线.
(2)解:过O作OM⊥AB于M.即∠OMA=90°,AM=BM,
∵∠MDC=∠OMA=∠DCO=90°,
∴四边形DMOC是矩形,
∴OC=DM,OM=CD.
∵AE=26,
∴AO=13,
∴OC=AO=13,
∴DM=13,
∴AM=13﹣DA,
∵DC+DA=6,
∴OM=CD=6﹣DA,
∵在Rt△AMO中,∠AMO=90°,根据勾股定理得:AO2=AM2+OM2.
∴132=(6﹣DA)2+(13﹣DA)2,
∴DA=1或DA=18(舍去),
∴AM=13﹣1=12,
∴AB=2AM=24.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
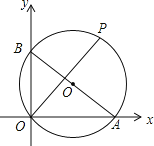
【题目】如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )
A.(8,6) B.(7,7) C.(7![]() ,7
,7![]() ) D.(5
) D.(5![]() ,5
,5![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】资阳市2012年财政收入取得重大突破,地方公共财政收入用四舍五入取近似值后为27.39亿元,那么这个数值【 】
A.精确到亿位 B.精确到百分位 C.精确到千万位 D.精确到百万位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O是坐标原点,点A的坐标是(-a,a),点B的坐标是(c,b),满足![]() .
.
(1)若x=2是3x-a<0的一个解,试判断点A在第几象限,并说明理由;
(2)若△AOB的面积是4,求点B的坐标;
(3)若两个动点E( e ,2e + 1) 、F( f ,-2f +3) ,请你探索是否存在以两个动点E、F为端点的线段EF∥AB,且EF=AB.若存在,求出E、F两点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论正确的是( )
A.若a2=b2 , 则a=b
B.若a>b,则a2>b2
C.若a,b不全为零,则a2+b2>0
D.若a≠b,则a2≠b2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com