
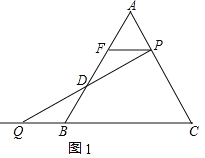
【题目】(阅读)如图1,等边△ABC中,P是AC边上一点,Q是CB延长线上一点,若AP=BQ.则过P作PF∥BC交AB于F,可证△APF是等边三角形,再证△PDF≌QDB可得D是FB的中点.请写出证明过程.
(运用)如图2,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A,C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.

(1)当∠BQD=30°时,求AP的长;
(2)在运动过程中线段ED的长是否发生变化?如果不变,直接写出线段ED的长;如果发生改变,请说明理由.
【答案】“阅读”详见解析;“运用”(1)AP=2;(2)运动过程中线段ED的长始终为3.
【解析】
【阅读】
:由△ABC是等边三角形和PF∥BC可得PF=BQ,进而证△PFD≌△QBD得DF=DB.
【运用】:(1)由△ABC是边长为6的等边三角形,可知∠ACB=60°,再由∠BQD=30°可知∠QPC=90°,设AP=x,则PC=6-x,QB=x,在Rt△QCP中,∠BQD=30°,PC=![]() QC,即6-x=
QC,即6-x=![]() (6+x),求出x的值即可;
(6+x),求出x的值即可;
(2)作QG⊥AB,交直线AB于点G,连接QE,PG,由点P、Q做匀速运动且速度相同,可知AP=BQ,再根据全等三角形的判定定理得出△APE≌△BQG,再由AE=BG,PE=QG且PE∥QG,可知四边形PEQG是平行四边形,进而可得出EB+AE=BE+BG=AB,DE=![]() AB,由等边△ABC的边长为6,可得出DE=3.
AB,由等边△ABC的边长为6,可得出DE=3.
解:【阅读】证明:如图1中,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵PF∥BC,
∴∠AFP=∠APF=∠ABC=∠ACB=60°,
∴AP=PF,
∵AP=BQ,
∴PF=BQ,
∵PF∥BQ,
∴∠FPD=∠DQB,∠PFD=∠QBD,
在△PFD与△QBD中,
 ,
,
∴△PFD≌△QBD;
∴DF=DB.
【运用】
:解:(1)如图2中,

∵△ABC是边长为6的等边三角形,
∴∠ACB=60°,
∵∠BQD=30°,
∴∠QPC=90°,
设AP=x,则PC=6﹣x,QB=x,
∴QC=QB+BC=6+x,
∵在Rt△QCP中,∠BQD=30°,
∴PC=![]() QC,即6﹣x=
QC,即6﹣x=![]() (6+x),解得x=2,
(6+x),解得x=2,
∴AP=2;
(2)作QG⊥AB,交直线AB于点G,连接QE,PG,

又∵PE⊥AB于E,
∴∠PGQ=∠AEP=90°,
∵点P、Q速度相同,
∴AP=BQ,
∵△ABC是等边三角形,
∴∠A=∠ABC=∠GBQ=60°,
在△APE和△BQG中,
∵∠AEP=∠BGQ=90°,
∴∠APE=∠BQG,
 ,
,
∴△APE≌△BQG(AAS),
∴AE=BG,PE=QG且PE∥QG,
∴四边形PEQG是平行四边形,
∴DE=![]() EG,
EG,
∵EB+AE=BE+BG=AB,
∴DE=![]() AB,
AB,
又∵等边△ABC的边长为6,
∴DE=3,
故运动过程中线段ED的长始终为3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点O是边AB、AC垂直平分线的交点,点E是∠ABC、∠ACB角平分线的交点,若∠O+∠E=180°,则∠A=_____度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对学生进行爱国主义教育,某校组织学生去看演出,有甲乙两种票,已知甲乙两种票的单价比为4:3,单价和为42元.
(1)甲乙两种票的单价分别是多少元?
(2)学校计划拿出不超过750元的资金,让七年级一班的36名学生首先观看,且规定购买甲种票必须多于15张,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为S,作△ABC边中线AC1,取AB的中点A1,连接A1C1得到第一个三角形△A1BC1,作△A1BC1中线A1C2,取A1B的中点A2,连接A1C2得到第二个三角形△A2BC2………,重复这样的操作,则第2019个三角形△A2019BC2019的面积是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
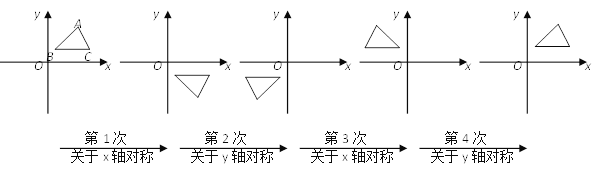
【题目】如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(2,3),则经过第2018次变换后所得的A点坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形纸片![]() 中,
中,![]() ,折叠纸片,使得点
,折叠纸片,使得点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕为
处,折痕为![]() ,点
,点![]() 分别在边
分别在边![]() 和
和![]() 上,当点
上,当点![]() 恰好是
恰好是![]() 边的中点时,点
边的中点时,点![]() 与点
与点![]() 重合,若在折叠过程中
重合,若在折叠过程中![]() ,则
,则![]() 等于________
等于________![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com