
【题目】小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC长2![]() ,钓竿AO的倾斜角∠ODC是60°,其长OA为5米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
,钓竿AO的倾斜角∠ODC是60°,其长OA为5米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
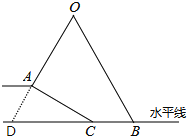
【答案】浮漂B与河堤下端C之间的距离为3米.
【解析】
试题分析:先根据三角形内角和定理求出∠CAD=180°﹣∠ODB﹣∠ACD=90°,解Rt△ACD,得出AD=ACtan∠ACD=2米,CD=2AD=3米,再证明△BOD是等边三角形,得到BD=OD=OA+AD=7米,然后根据BC=BD﹣CD即可求出浮漂B与河堤下端C之间的距离.
解:∵AO的倾斜角是60°,
∴∠ODB=60°.
∵∠ACD=30°,
∴∠CAD=180°﹣∠ODB﹣∠ACD=90°.
在Rt△ACD中,AD=ACtan∠ACD=2![]() ×
×![]() =2(米),
=2(米),
∴CD=2AD=4米,
又∵∠O=60°,
∴△BOD是等边三角形,
∴BD=OD=OA+AD=2+5=7(米),
∴BC=BD﹣CD=7﹣4=3(米).
答:浮漂B与河堤下端C之间的距离为3米.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=(x﹣1)2﹣1与双曲线y=![]() 交于点A(﹣1,m).
交于点A(﹣1,m).

(1)求k与m的值;
(2)写出点A关于抛物线y=(x﹣1)2﹣1的对称轴的对称点坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解一批产品的质量,从中抽取300个产品进行检验,在这个问题中,被抽取的300个产品叫做( )
A. 总体 B. 个体 C. 总体的一个样本 D. 普查方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过A (1,0)、B(0,3)及C(3,0)点,动点D从原点O开始沿OB方向以每秒1个单位长度移动,动点E从点C开始沿CO方向以每秒1个长度单位移动,动点D、E同时出发,当动点E到达原点O时,点D、E停止运动.
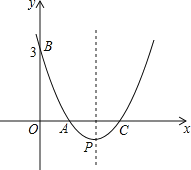
(1)求抛物线的解析式及顶点P的坐标;
(2)若F(﹣1,0),求△DEF的面积S与E点运动时间t的函数解析式;当t为何值时,△DEF的面积最大?最大面积是多少?
(3)当△DEF的面积最大时,抛物线的对称轴上是否存在一点N,使△EBN是直角三角形?若存在,求出N点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)![]()
(2)(﹣a)2 ![]() a4÷a3
a4÷a3
(3)(2x﹣1)(x﹣3)
(4)(3x﹣2y)2(3x+2y)2
(5)(x﹣2y+4)(x﹣2y﹣4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com