
【题目】如图,已知抛物线y=ax2+bx+c经过A (1,0)、B(0,3)及C(3,0)点,动点D从原点O开始沿OB方向以每秒1个单位长度移动,动点E从点C开始沿CO方向以每秒1个长度单位移动,动点D、E同时出发,当动点E到达原点O时,点D、E停止运动.
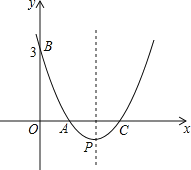
(1)求抛物线的解析式及顶点P的坐标;
(2)若F(﹣1,0),求△DEF的面积S与E点运动时间t的函数解析式;当t为何值时,△DEF的面积最大?最大面积是多少?
(3)当△DEF的面积最大时,抛物线的对称轴上是否存在一点N,使△EBN是直角三角形?若存在,求出N点的坐标,若不存在,请说明理由.
【答案】(1)y=x2﹣4x+3,(2,﹣1);(2)当t=2时,S最大=2;(3)N点的坐标(2,2),(2,1),(2,![]() ),(2,
),(2,![]() ).
).
【解析】
试题分析:(1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;
(2)根据三角形的面积公式,可得函数解析式,根据二次函数的性质,可得答案;
(3)根据勾股定理的逆定理,可得关于a的方程,根据解方程,可得N点坐标.
解:(1)将A (1,0)、B(0,3)及C(3,0)代入函数解析式,得
 ,
,
解得 ,
,
抛物线的解析式为y=x2﹣4x+3,
配方,得y=(x﹣2)2﹣1,顶点P的坐标为(2,﹣1);
(2)如图1
 ,
,
由题意,得
CE=t,OE=3﹣t,FE=4﹣t,OD=t.
S=![]() FEOD=
FEOD=![]() (4﹣t)t=﹣
(4﹣t)t=﹣![]() t2+2t=﹣
t2+2t=﹣![]() (t﹣2)2+2,
(t﹣2)2+2,
当t=2时,S最大=2;
(3)当△DEF的面积最大时,E(1,0),设N(2,a),
BN2=4+(a﹣3)2,EN2=1+a2,BE2=1+9=10,
①当BN2+EN2=BE2时,4+9﹣6a+a2+a2+1=10,化简,得
a2﹣3a+2=0,解得a=2,a=1,N(2,2),N(2,1);
②当BN2+BE2=EN2时,4+9﹣6a+a2+10=1+a2,化简,得
6a=22,解得a=![]() ,N(2,
,N(2,![]() );
);
③当BE2+EN2=BN2时,1+a2+10=4+9﹣6a+a2,
化简,得
6a=2,解得a=![]() ,N(2,
,N(2,![]() ),
),
综上所述:N点的坐标(2,2),(2,1),(2,![]() ),(2,
),(2,![]() ).
).


科目:初中数学 来源: 题型:
【题目】在天文学上,计算星球之问的距离通常用“光年”作单位,1光年即光在一年内通过的路程.已知光的速度是3×105km/s,一年约为3×107s,则1光年约等于( )
A. 9×1012km B. 6×1035km C. 6×1012km D. 9×1035km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数中x和y的部分对应值如下表:
x … ﹣1 0 1 2 3 …
y … 0 ﹣3 ﹣4 ﹣3 0 …
(1)求二次函数的解析式;
(2)如图,点P是直线BC下方抛物线上一动点,当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积;

(3)在抛物线上,是否存在一点Q,使△QBC中QC=QB?若存在请直接写出Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
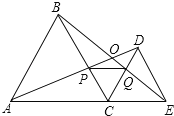
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
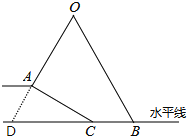
【题目】小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC长2![]() ,钓竿AO的倾斜角∠ODC是60°,其长OA为5米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
,钓竿AO的倾斜角∠ODC是60°,其长OA为5米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数与反比例函数的图象交于点A(﹣4,﹣2)和B(a,4).
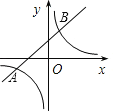
(1)求反比例函数的解析式和点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com