
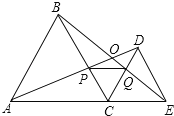
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)
【答案】①②③⑤
【解析】
试题分析:由已知条件运用等边三角形的性质得到三角形全等,进而得到更多结论,然后运用排除法,对各个结论进行验证从而确定最后的答案.
解:①∵正△ABC和正△CDE,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACD=∠ACB+∠BCD,∠BCE=∠DCE+∠BCD,
∴∠ACD=∠BCE,
∴△ADC≌△BEC(SAS),
∴AD=BE,∠ADC=∠BEC,(故①正确);
②又∵CD=CE,∠DCP=∠ECQ=60°,∠ADC=∠BEC,
∴△CDP≌△CEQ(ASA).
∴CP=CQ,
∴∠CPQ=∠CQP=60°,
∴∠QPC=∠BCA,
∴PQ∥AE,(故②正确);
③∵△CDP≌△CEQ,
∴DP=QE,
∵△ADC≌△BEC
∴AD=BE,
∴AD﹣DP=BE﹣QE,
∴AP=BQ,(故③正确);
④∵DE>QE,且DP=QE,
∴DE>DP,(故④错误);
⑤∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,(故⑤正确).
∴正确的有:①②③⑤.
故答案为:①②③⑤.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
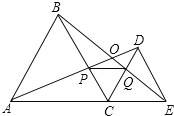
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标。(2)求出S△ABC(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△A′B′C′,并写出A′、B′、C′的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是四边形ABCD的边AB上一点.
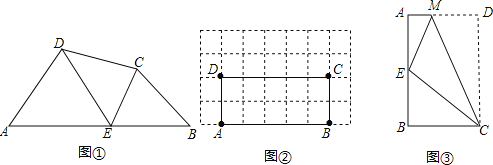
(1)猜想论证:如图,分别连接DE、CE,若∠A=∠B=∠DEC=65°,试猜想图中哪两个三角形相似,并说明理由.
(2)观察作图:如图,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图中矩形ABCD的边AB上画出所有满足条件的点E(点E与点A,B 不重合),分别连结ED,EC,使四边形ABCD被分成的三个三角形相似(不证明).
(3)拓展探究:如图,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好将四边形ABCM分成的三个三角形相似,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过A (1,0)、B(0,3)及C(3,0)点,动点D从原点O开始沿OB方向以每秒1个单位长度移动,动点E从点C开始沿CO方向以每秒1个长度单位移动,动点D、E同时出发,当动点E到达原点O时,点D、E停止运动.
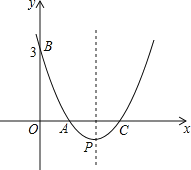
(1)求抛物线的解析式及顶点P的坐标;
(2)若F(﹣1,0),求△DEF的面积S与E点运动时间t的函数解析式;当t为何值时,△DEF的面积最大?最大面积是多少?
(3)当△DEF的面积最大时,抛物线的对称轴上是否存在一点N,使△EBN是直角三角形?若存在,求出N点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )
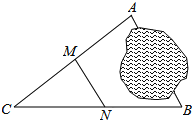
A.MN∥AB
B.AB=24m
C.△CMN∽△CAB
D.△CMN与四边形ABMN的面积之比为1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.

(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
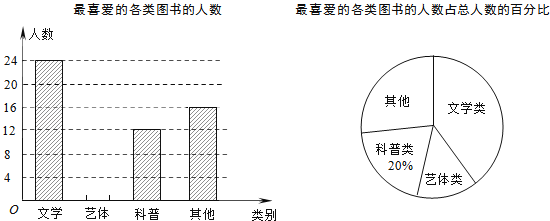
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com