
【题目】如图,E是四边形ABCD的边AB上一点.
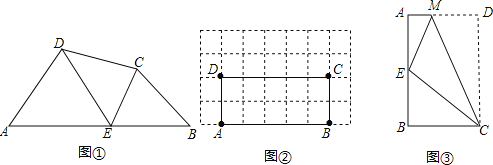
(1)猜想论证:如图,分别连接DE、CE,若∠A=∠B=∠DEC=65°,试猜想图中哪两个三角形相似,并说明理由.
(2)观察作图:如图,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图中矩形ABCD的边AB上画出所有满足条件的点E(点E与点A,B 不重合),分别连结ED,EC,使四边形ABCD被分成的三个三角形相似(不证明).
(3)拓展探究:如图,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好将四边形ABCM分成的三个三角形相似,请直接写出![]() 的值.
的值.
【答案】(1)△ADE∽△BEC;(2)见解析;(3)![]() =
=![]() .
.
【解析】
试题分析:(1)△ADE∽△BEC,理由为:利用三角形内角和定理及邻补角定义得到一对角相等,再由已知角相等,利用两角相等的三角形相似即可得证;
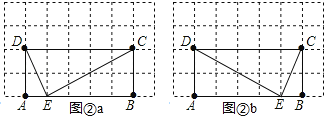
(2)如图②a与图②b所示,点E为所求的点;
(3)由点E恰好将四边形ABCM分成的三个三角形相似,利用相似三角形对应角相等得到三个角相等,再由折叠的性质得到∠DCM=∠MCE=∠BCE=30°,EC=CD=AB,在Rt△BCE中,利用锐角三角函数定义求出所求式子比值即可.
解:(1)△ADE∽△BEC,理由为:
∵∠A=65°,
∴∠ADE+∠DEA=115°,
∵∠DEC=65°,
∴∠BEC+∠DEA=115°,
∴∠ADE=∠BEC,
∵∠A=∠B,
∴△ADE∽△BEC;
(2)作图如下:
(3)∵点E恰好将四边形ABCM分成的三个三角形相似,
∴△AEM∽△BCE∽△ECM,
∴∠BCE=∠ECM=∠AEM,
由折叠可知:△ECM≌△DCM,
∴∠ECM=∠DCM,CE=CD,
∴∠BCE=∠ECM=∠DCM=30°,
∴DC=CE=AB,
在Rt△BCE中,cos∠BCE=![]() =cos30°,
=cos30°,
∴![]() =
=![]() .
.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】根据下列条件,能判定一个三角形是直角三角形的是( )
A.三条边的边长之比是1:2:3
B.三个内角的度数之比是1:1:2
C.三条边的边长分别是![]() ,
,![]() ,
,![]()
D.三条边的边长分别是12,15,20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】所谓配方,就是把一个多项式经过适当变形配成完全平方式.配方法除一元二次方程求根公式推导这一典型应用外,在因式分解、化简二次根式、证明恒等式、解方程、求代数式最值等问题中都有广泛应用.是一种很重要、很基本的数学方法.如以下例1,例2:
例1:分解因式 x2﹣120x+3456
解:原式=x2﹣120x+3600+3456﹣3600
=(x﹣60)2﹣144
=(x﹣60+12)(x﹣60﹣12)
=(x﹣48)(x﹣72)
例2:化简:![]()
解:原式=![]()
=![]()
=![]() ﹣
﹣![]()
阅读以上材料,请问答以下问题:
(1)分解因式:x2﹣40x+319= ;
(2)化简:![]() ;
;
(3)利用配方法求4x2+y2﹣2y﹣4x+15的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有客房200间供游客居住,当每间客房的定价为每天180元时,客房恰好全部住满;如果每间客房每天的定价每增加10元,就会减少4间客房出租.设每间客房每天的定价增加![]() 元,宾馆出租的客房为
元,宾馆出租的客房为![]() 间.求:
间.求:
(1)![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果某天宾馆客房收入38400元,那么这天每间客房的价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
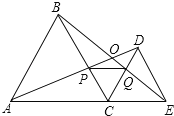
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形两边长分别是2 cm和5 cm,则这个三角形周长是( )
A. 9 cm B. 12 cm C. 9 cm或12 cm D. 14 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:
①如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;
②如果直角三角形的两边是5、12,那么斜边必是13;
③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边是a,b,c(a>b=c),那么a2:b2:c2=2:1:1.
其中正确的是( )
A.①② B.①③ C.①④ D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
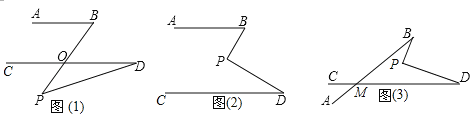
【题目】(1)、如图(1),AB∥CD,点P在AB、CD外部,若∠B=40°,∠D=15°,则∠BPD °.
(2)、如图(2),AB∥CD,点P在AB、CD内部,则∠B,∠BPD,∠D之间有何数量关系?证明你的结论;
(3)、在图(2)中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图(3),若∠BPD=90°,∠BMD=40°,求∠B+∠D的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com