
����Ŀ����֪���κ�����x��y�IJ��ֶ�Ӧֵ���±���
x �� ��1 0 1 2 3 ��
y �� 0 ��3 ��4 ��3 0 ��
��1������κ����Ľ���ʽ��
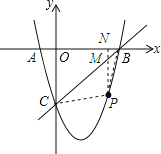
��2����ͼ����P��ֱ��BC�·���������һ���㣬����P�˶���ʲôλ��ʱ���ı���ABPC�������������ʱP���������ı���ABPC����������

��3�����������ϣ��Ƿ����һ��Q��ʹ��QBC��QC=QB����������ֱ��д��Q������꣮
���𰸡���1��y=x2��2x��3����2��P��![]() ����
����![]() ����
����![]() ����3��Q1��
����3��Q1��![]() ����
����![]() ����Q2��
����Q2��![]() ����
����![]() ����
����
��������
�����������1�����ô���ϵ����������ö��κ����Ľ���ʽ��
��2���������ֱ��BC�Ľ���ʽ����P��PN��x�ύֱ��BC�ڵ�M��Ȼ�����S��BPC=S��PCM+S��PMB=![]() PMON+
PMON+![]() PMNB�����ɰ�S��BPC��ʾ��P�ĺ�����x�ĺ��������ݺ�������������ֵ��
PMNB�����ɰ�S��BPC��ʾ��P�ĺ�����x�ĺ��������ݺ�������������ֵ��
��3��QC=QB����Q�����߶�BC���д�������κ����Ľ��㣬�������BC�Ľ���ʽ��Ȼ��ⷽ���鼴�ɣ�
�⣺��1����y=a��x+1����x��3���ѣ�0����3������ɵã���3=a��0+1����0��3��
��ã�a=1��y=��x+1����x��3��=x2��2x��3��
�����κ����Ľ���ʽΪ��y=x2��2x��3��
��2��S�ı���ABPC=S��ABC+S��BPC=![]() ��1��3+S��BPC��
��1��3+S��BPC��
��ֱ��BC�Ľ���ʽ��y=kx+b��
��![]() ��
��
��ã�![]() ��
��
��ֱ��BC�Ľ���ʽ�ǣ�y=x��3��
��P��PN��x�ύֱ��BC�ڵ�M����P��x��x2��2x��3����M��x��x��3��
��MP=x��3����x2��2x��3��=��x2+3x
S��BPC=S��PCM+S��PMB=![]() PMON+
PMON+![]() PMNB
PMNB
=![]() PMOB=
PMOB=![]() ����x2+3x����3=��
����x2+3x����3=��![]() x2+
x2+![]() x=��
x=��![]() ��x��
��x��![]() ��2+
��2+![]() ��0��x��3����
��0��x��3����
��x=![]() ʱ��S��BPC�����ֵΪ
ʱ��S��BPC�����ֵΪ![]() ���� S�ı���ABPC�����ֵΪ��
���� S�ı���ABPC�����ֵΪ��![]() +
+![]() =
=![]() ��
��
��ʱP��![]() ����
����![]() ����
����
��3��BC���е������ǣ�![]() ����
����![]() ����
����
���߶�BC���д��ߵĽ���ʽ��y=��x+c����![]() +c=��
+c=��![]() ��
��
���c=0��
��BC���д��ߵĽ���ʽ��y=��x��
��������ã�![]() ��
��
��ã�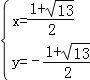 ��
�� ��
��
��Q�������ǣ�Q1��![]() ����
����![]() ����Q2��
����Q2��![]() ����
����![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���������У���ͳһ�滮����һ�����β�ƺ���ϱ���������3m��������������3m��������ij����β�ƺ�����ԭ�������β�ƺ�����ȣ�������
A. ����6m2 B. ����6m2 C. ����9m2 D. ����9m2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ҽԺסԺ��������10�����ij���˵�������36�������²�������Ϊ��0.2, 0.3, 0.1, 0.1, 0, 0.2, 0.1, 0.1, 0.1, 0,�����10���иò��˵����²������ݷ�������ȷ����( )
A. ƽ����Ϊ0.12 B. ����Ϊ0.1
C. ��λ��Ϊ0.1 D. ����Ϊ0.02
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�鳤80�L����60�L����Ƥ��4���Ƿֱ��ȥһ���߳���ȵ�С�����Σ�����һ���������1500�L2�������С�����С�����εı߳�Ϊx�L���������еķ����У���ȷ���ǣ� ��.
A.��80��x����60��x��=1500
B.��80��2x����60��2x��=1500
C.��80��2x����60��x��=1500
D.��80��x����60��2x��=1500
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x��1��2��1��˫����y=![]() ���ڵ�A����1��m����
���ڵ�A����1��m����

��1����k��m��ֵ��
��2��д����A����������y=��x��1��2��1�ĶԳ���ĶԳƵ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�е�P��-1��2��һ���ڣ� ��
A. ��һ���� B. �ڶ����� C. �������� D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c����A ��1��0����B��0��3����C��3��0���㣬����D��ԭ��O��ʼ��OB������ÿ��1����λ�����ƶ�������E�ӵ�C��ʼ��CO������ÿ��1�����ȵ�λ�ƶ�������D��Eͬʱ������������E����ԭ��Oʱ����D��Eֹͣ�˶���
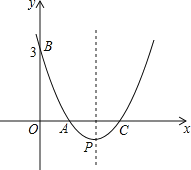
��1���������ߵĽ���ʽ������P�����ꣻ
��2����F����1��0��������DEF�����S��E���˶�ʱ��t�ĺ�������ʽ����tΪ��ֵʱ����DEF���������������Ƕ��٣�
��3������DEF��������ʱ�������ߵĶԳ������Ƿ����һ��N��ʹ��EBN��ֱ�������Σ������ڣ����N������꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����գ���ͼ������ֽ��ÿ��С�����εı߳���Ϊ1���ڷ���ֽ�ڽ���ABC����һ��ƽ�ƺ�õ���A��B��C����ͼ�б���˵�B�Ķ�Ӧ��B�䣮
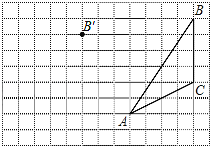
��1���ڸ�������ֽ�л���ƽ�ƺ����A��B��C����
��2������AB���ϵ�����CD��BC���ϵĸ���AE��
��3���߶�AA�����߶�BB��Ĺ�ϵ�ǣ� ��
��4������A��B��C���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com