
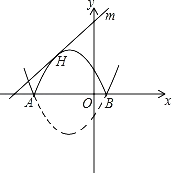
����Ŀ����ͼ����֪���κ���L��y��mx2+2mx+k������m��k�dz�����kΪ����������
��1����L�����㣨1��k+6������m��ֵ��
��2����m��2����L��x���й�����ʱ�ҹ�����ĺ�����Ϊ�����������ȷ��k��ֵ��
��3���ڣ�2���������½�L��y��mx2+2mx+k��ͼ������ƽ��8����λ���õ�����ͼ��M����M�Ľ���ʽ��
��4����M��ͼ����x���·��IJ�����x�ᷭ�ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ���µ�ͼ��N�������µ�ͼ�������⣬��ֱ��y��![]() x+b��N������������ʱ����ֱ��д��b��ȡֵ��Χ��
x+b��N������������ʱ����ֱ��д��b��ȡֵ��Χ��

���𰸡���1��m��2����2��k��2����3��y��2x2+4x��6������4����![]() ��b��
��b��![]() ��b��
��b��![]() ��
��
��������
��1�����㣨1��k+6������y��mx2+2mx+k��������⣻
��2��������ã�����16��8k��0��������⣻
��3������ƽ�ƵĹ�ʽ������⣻
��4��ȷ����H��A��B�����ٽ�㣬����ٽ��ʱb��ֵ��������⣮
�⣺��1�����㣨1��k+6������y��mx2+2mx+k����ã�
m��2��
��2��y��mx2+2mx+k��2x2+4x+k��
������ã�����16��8k��0����ã�k��2��
��kΪ����������k��1ʱ������û�������⣬����ȥ��
��k��2��
��3����m��2��k��2ʱ��y��2x2+4x+2������ƽ��8����λ��
ƽ�ƺ�ı���ʽΪ��y��2x2+4x+2��8��2x2+4x��6��
��4���ɣ�3��֪��M�ı���ʽΪ��y��2x2+4x��6����
���ۺ������ߵı���ʽΪ��y�䣽��2x2��4x+6����
��ֱ��mΪ��y��![]() x+b����
x+b����
����ֱ��m�뷭�ۺ��ͼ����һ�����㣨��H��ʱ������ͼ��
�����ڢ��������ã�2x2+![]() x+b��6��0��
x+b��6��0��
�����![]() ��8��b��6����0����ã�b��
��8��b��6����0����ã�b��![]() ��
��
����ֱ��m����A����3��0��ʱ��
����A�����������ʽ�ã�0��![]() ������3��+b����ã�b��
������3��+b����ã�b��![]() ��
��
����ֱ��m����Bʱ��
ͬ���ɵã�b����![]() ��
��
��ֱ��y��![]() x+b��N������������ʱ��b��ȡֵ��ΧΪ����
x+b��N������������ʱ��b��ȡֵ��ΧΪ����![]() ��b��
��b��![]() ��b��
��b��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ר��һ��綯��ˢ����ɱ�Ϊ20Ԫ/֧�������з��֣�����Ʒÿ���������y(֧�������۵���x(Ԫ/֧��֮�������ͼ��ʾ�Ĺ�ϵ��
(1)��y��x֮��ĺ�����ϵʽ��
(2)���ں���ʡ�人�б���������״�������ף�������¹ڷ����������飬���������������ÿ���õ������г��200Ԫ�����人��Ϊ�˱�֤����ÿ��ʣ��������550Ԫ�����ȷ�����綯��ˢ�����۵��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
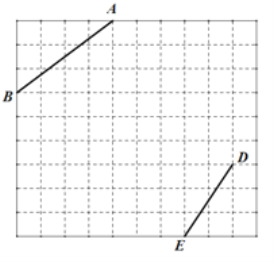
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳���Ϊ 1���߶� AB��DE �Ķ˵� A��B��D��E ����С�����εĶ����ϣ�
��1����ͼ�л�һ���� AB Ϊһ���ĵ�����ABC�� ��tan ABC ![]() ����C ��С�����εĶ����ϣ�
����C ��С�����εĶ����ϣ�
��2����ͼ�л�һ���� DE Ϊ�ߵ�ƽ���ı��� DEFG����G 45�� ���� F��G ����С�����εĶ����ϣ����� CG����ֱ��д���߶� CG �ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
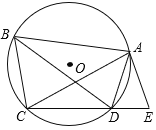
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O����֪AB��AC���ӳ�CD����E��ʹCE��BD������AE��
��1����֤��ADƽ�֡�BDE��
��2����AB��CD����֤��AE�ǡ�O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Сʢ��������ѧ��������������������ѧ��Ϸ
��1���涨���ĸ����ظ�������ֵС��![]() ����������ͨ���ӷ������������
����������ͨ���ӷ������������![]()
Сʢ��![]() ��������
��������![]() �����Ƿ�����������ʽ���������д����һ�������û�У����˵�����ɣ�
�����Ƿ�����������ʽ���������д����һ�������û�У����˵�����ɣ�
��2���涨���ĸ����ظ�������ֵС![]() ��������ͨ���ӷ����������
��������ͨ���ӷ����������![]()
Сʢ��![]() ��������
��������![]() �������Ҫ����д��һ�������Dz�ͬ����ʽ��
�������Ҫ����д��һ�������Dz�ͬ����ʽ��
��3���ã�2����Сʢ����������ʽ����������ȥ���һ�����У�ʹ���ڵ��ĸ����ĺͶ�����![]() ��Сʢ��
��Сʢ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
![]()
������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
![]()
��![]() ______��
______��![]() _______��������д�������е�ǰ
_______��������д�������е�ǰ![]() ��ĺͣ�
��ĺͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڿ����¹ڷ��������ڼ䣬�ϰ���Խ��Խ��������������ȡ��Ҫ���������ϣ�Сʯ��Ӫ��ˮ����Ҳ��ʱ������ij����ƽ̨���������۵�ˮ���еIJ��֣����±������д��������������ˮ�������ͷ���һ�ι���ˮ�����ܼ���128Ԫ��![]() Ԫ��ÿ�ʶ����˿�����֧���ɹ���Сʯ��õ�֧�����80%��
Ԫ��ÿ�ʶ����˿�����֧���ɹ���Сʯ��õ�֧�����80%��
�������ˮ�� | |
ˮ�� | ����ǰ���� |
ƻ�� | 58Ԫ/�� |
�ҰҸ� | 70Ԫ/�� |
������ | 100Ԫ/�� |
������ | 48Ԫ/�� |
��1����![]() ʱ��ij�˿�һ�ι���ƻ���ͳ����Ӹ�1�䣬��Ҫ֧��_____Ԫ��Сʯ��õ�______Ԫ��
ʱ��ij�˿�һ�ι���ƻ���ͳ����Ӹ�1�䣬��Ҫ֧��_____Ԫ��Сʯ��õ�______Ԫ��
��2���ڴ�����У�Ϊ����Сʯÿ�ʶ������õ��Ľ����ڴ���ǰ�ܼ۵����ۣ���![]() �����ֵΪ_____��
�����ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD���Ե�AΪԲ�ģ�С��AC��Ϊ�뾶��Բ�����ֱ�AB��AC��E��F���㣬�ٷֱ���E��FΪԲ�ģ�����![]() EF��Ϊ�뾶��Բ��������Բ�����ڵ�P������AP����CD�ڵ�M������ACD��110�������CMA�Ķ���Ϊ��������
EF��Ϊ�뾶��Բ��������Բ�����ڵ�P������AP����CD�ڵ�M������ACD��110�������CMA�Ķ���Ϊ��������
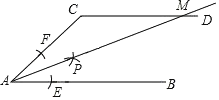
A.30��B.35��C.70��D.45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij��2015����б�ҵ����ѧ�������ɼ��ȼ��ķֲ�����������ȡ�˸������������б�ҵ������ѧ�������ɼ�����A��B��C��D�ĸ��ȼ�����ͳ�Ʒ������������������в�������ͳ��ͼ��

���������ͳ��ͼ�ṩ����Ϣ������������⣺
��1�����γ�ȡ��ѧ������ ��������ȫ����ͳ��ͼ1��
��2�����ݵ�����������Ƹ���1430�����б�ҵ����ѧ�������ɼ�ΪA����������
��3��ijУA�ȼ����мס��ҡ�������4��ѧ���ɼ����е�һ������Ҫ����4λѧ���г�ȡ2��ѧ����У����ѧϰ������ܣ����оٷ����ǡ��ѡ�м�����λѧ���ĸ��ʡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳���3����P��ֱ��BC��һ�㣬����PA�����߶�PA�Ƶ�P��ʱ����ת90���õ��߶�PE����ֱ��BA��ȡ��F��ʹBF=BP���ҵ�F���E��BCͬ�࣬����EF��CF��

��1����ͼ��������P��CB�ӳ�����ʱ����֤���ı���PCFE��ƽ���ı��Σ�
��2����ͼ��������P���߶�BC��ʱ���ı���PCFE�Ƿ���ƽ���ı��Σ�˵�����ɣ�
��3���ڣ�2���������£��ı���PCFE������Ƿ������ֵ�����У��������������ֵ����ʱBP������û�У���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com