
����Ŀ��Сʢ��������ѧ��������������������ѧ��Ϸ
��1���涨���ĸ����ظ�������ֵС��![]() ����������ͨ���ӷ������������
����������ͨ���ӷ������������![]()
Сʢ��![]() ��������
��������![]() �����Ƿ�����������ʽ���������д����һ�������û�У����˵�����ɣ�
�����Ƿ�����������ʽ���������д����һ�������û�У����˵�����ɣ�
��2���涨���ĸ����ظ�������ֵС![]() ��������ͨ���ӷ����������
��������ͨ���ӷ����������![]()
Сʢ��![]() ��������
��������![]() �������Ҫ����д��һ�������Dz�ͬ����ʽ��
�������Ҫ����д��һ�������Dz�ͬ����ʽ��
��3���ã�2����Сʢ����������ʽ����������ȥ���һ�����У�ʹ���ڵ��ĸ����ĺͶ�����![]() ��Сʢ��
��Сʢ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
![]()
������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
![]()
��![]() ______��
______��![]() _______��������д�������е�ǰ
_______��������д�������е�ǰ![]() ��ĺͣ�
��ĺͣ�
���𰸡���1��û�У����ɼ���������2��![]() ���𰸲�Ψһ������3��
���𰸲�Ψһ������3��![]() ��
��![]() �����е�ǰ
�����е�ǰ![]() ���Ϊ
���Ϊ![]() ��
��
��������
��1������1+2+3+4=10��Ҫ��Ϊ12���ڴ˻����ϼ�2���ɴ�˼���ó����ۣ�
��2������-2-3+8+9=12�ϱ仯���������ԣ�
��3���ܹ���Ϊ12���㣬��ɵ�x��y������д������ÿ4����Ϊһ�������ظ����֣����˹��ɵ�ǰ4������16�����Ϊ12��4���ټ��ϵ�5���ǰ3������ɵ�ǰ19��ĺͣ�
�⣺��1��û��������ʽ�ˣ�
�ĸ�С��![]() ��ͬ����������С�ĺ�Ϊ
��ͬ����������С�ĺ�Ϊ![]() ��Ҫ��õ���Ϊ
��Ҫ��õ���Ϊ![]() ����Ҫ��
����Ҫ��![]() ��
��
���κ���������![]() ��������һ������
��������һ������![]() ��
��
����Ϊ���ֲ����ظ���
����ֻ����![]() ��4+1��3+2����4+2��
��4+1��3+2����4+2��
�ʷ�����������ʽ��![]() ��
��![]() ��ֻ������
��ֻ������
��2��������ɵã�![]() ��
��
��3��������ã�x=12-��-3+8+9��=-2��
y=12-��0+8+7��=-3��
������֪������д������ÿ4������-3��0��8��7��Ϊһ�������ظ����֣�
��19��4=4��3��
������д�������е�ǰ19��ĺ�=12��4+��-3+0+8��=53��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��BΪֱ��y��x�ϵ����㣬��A��B����ֱ���y���ƽ���߽�˫����![]() ��x��0���ڵ�C��D���㣮��BD��2AC����4OC2��OD2��ֵΪ�� ��
��x��0���ڵ�C��D���㣮��BD��2AC����4OC2��OD2��ֵΪ�� ��

A.5B.6C.7D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�з���һ��������ߣ��ɱ�Ϊÿ��50Ԫ��Ͷ���г����������ۣ������۵��۲����ڳɱ���������۲��Ź涨�����������ʲ�����70%���г����з��֣���һ��ʱ���ڣ�ÿ����������y�����������۵���x��Ԫ����xΪ����������һ�κ�����ϵ����ͼ��ʾ
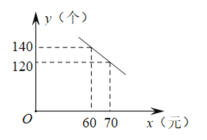
��1�����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2���ù�˾Ҫ��ÿ����3000Ԫ�������������۵���Ӧ��Ϊ����Ԫ��
��3�����۵���Ϊ����Ԫʱ��ÿ���õ����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ij�ֶ�ͯ��ߣ����ÿ������Ϊ40Ԫ���г��������Ź涨���������ÿ�������ܳ���60Ԫ����ÿ����۳�50���������г����鷢�֣����۵���ÿ����2Ԫ��ÿ�������������1���������۵�������![]() Ԫ��ÿ���۳�
Ԫ��ÿ���۳�![]() ����
����
��1�����![]() ��
��![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
��2����![]() Ϊ����ʱ������ÿ������������߿ɻ�����2250Ԫ��
Ϊ����ʱ������ÿ������������߿ɻ�����2250Ԫ��
��3���賬��ÿ������������߿ɻ���![]() Ԫ����
Ԫ����![]() Ϊ����ʱ
Ϊ����ʱ![]() ������ֵ�Ƕ��٣�
������ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȫ�潨��С�����͡�ʮ���塱�滮�չ�֮�꣬Ϊ�ٽ����ۣ�ij��˾������A��B�����²�Ʒ������ǰ����������֪A��B�ijɱ����ۼۺ�ÿ���������±���ʾ��
�ɱ���Ԫ/���� | �ۼۣ�Ԫ/���� | ��������/�գ� | |
A | 500 | 700 | 500 |
B | 800 | 1050 | 300 |
���������������˾��B���Ʒ�������ۣ�ͬʱ��A���Ʒ������ۣ�����B���Ʒÿ����5Ԫ�Ͷ�����2����A���Ʒÿ���5Ԫ�Ϳ�������1����Ҫ����ÿ�յ����������䣬��A���Ʒÿ��������x����ÿ���ܻ���ΪyԪ��
��1����y��x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2��Ҫʹÿ��������208000Ԫ��ֱ��д��x��ȡֵ��Χ��
��3���ù�˾����ÿ����һ��A��Ʒ���;����ʮ�ֻ�a��0��a��100��Ԫ��Ϊ�����𣮵�40��x��50ʱ��ÿ�յ��������Ϊ237250Ԫ����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���L��y��mx2+2mx+k������m��k�dz�����kΪ����������
��1����L�����㣨1��k+6������m��ֵ��
��2����m��2����L��x���й�����ʱ�ҹ�����ĺ�����Ϊ�����������ȷ��k��ֵ��
��3���ڣ�2���������½�L��y��mx2+2mx+k��ͼ������ƽ��8����λ���õ�����ͼ��M����M�Ľ���ʽ��
��4����M��ͼ����x���·��IJ�����x�ᷭ�ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ���µ�ͼ��N�������µ�ͼ�������⣬��ֱ��y��![]() x+b��N������������ʱ����ֱ��д��b��ȡֵ��Χ��
x+b��N������������ʱ����ֱ��д��b��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ŭ����������2019���������������ͬ�����ơ����������ϳ�����������������£�����������ϸ�����![]() ����������Ҫ��Ⱦ��ͬ�Ⱦ����Ը��ƶԱ����п����������й����ݽ����ռ����������������������������˲�����Ϣ��
����������Ҫ��Ⱦ��ͬ�Ⱦ����Ը��ƶԱ����п����������й����ݽ����ռ����������������������������˲�����Ϣ��
a��������2019���������������ֲ��������ͼ��ȫ����������Ⱦ�գ�������������

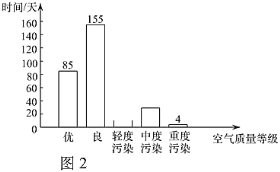
b��������2019����������ж�������![]() �������Ũ��Ϊ4��/�����ף��ȶ��ﵽ���Ҷ�������60��/�����ף���
�������Ũ��Ϊ4��/�����ף��ȶ��ﵽ���Ҷ�������60��/�����ף���![]() ������������
������������![]() �������Ũ���ֱ�Ϊ68��/�����ף�37��/�����ף����״δﵽ���Ҷ�������70��/�����ף�40��/�����ף���
�������Ũ���ֱ�Ϊ68��/�����ף�37��/�����ף����״δﵽ���Ҷ�������70��/�����ף�40��/�����ף���![]() �����Ũ��Ϊ
�����Ũ��Ϊ![]() �������ף����DZ����д�����Ҫ��Ⱦ��������Ҷ�������35��/�����ף���20%��
�������ף����DZ����д�����Ҫ��Ⱦ��������Ҷ�������35��/�����ף���20%��
c��������2019�����������![]() �¾�Ũ�ȱ仯������£�
�¾�Ũ�ȱ仯������£�
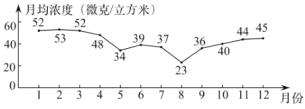
��������![]() ���¾�Ũ������λ����/�����ף����£�����������
���¾�Ũ������λ����/�����ף����£�����������
�·� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
�¾�Ũ�� | 9 | 6 | 5 | 4 | 3 | 2 | 3 | 3 | 5 | 4 |
������������Դ�ڱ�������̬�����ֹٷ���վ��
���������ţ��ش��������⣺
��1��������2019���������Ϊ�������Ⱦ������Ϊ�� ����
A��82 B��92 C��102
��2��![]() ��ֵ��______��
��ֵ��______��
��3��������2019�����������![]() �¾�Ũ���ﵽ���Ҷ������ĸ���Ϊ______��
�¾�Ũ���ﵽ���Ҷ������ĸ���Ϊ______��
��4��������2019�����������![]() �¾�Ũ����������4������λ����______��
�¾�Ũ����������4������λ����______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������2��27�չ���Ժ�������ŷ������ϣ��й��������ķ������ᵽ�������¹ڷ��ͷ������������������֣���ij��λ�������ɹ���һ��ҽ����ƿ��֣����۷ֱ�Ϊ1Ԫ��1.5Ԫ��3Ԫ��5Ԫ��10Ԫ��ÿ������䷢��ÿλ�ڸ�Ա��һ������.�ֽ�����10������䷢��������Ƴ�����ͳ�Ʊ���
�䷢��/�� | 30 | 25 | 20 | 15 |
����/�� | 2 |
|
| 1 |
��֪�䷢����ƽ������23������λ����![]() ����������
����������![]() ����
����
��1����![]() ��ֵ��������
��ֵ��������![]() ��
��
��2�����䷢15��������һ���в�ͬ�ͺŵĿ��ַ����������ͳ�ƣ����Ƴ���ͼ��ʾ���в�������ͳ��ͼ.��ȫͳ��ͼ������С����ò�����3Ԫ���ֵĸ��ʣ�
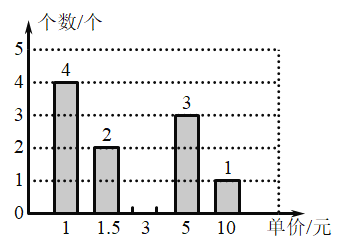
��3������������������֣�����12������䷢����������ǰ10������䷢����������ͬ�����磺ֻҪ�ڵ�11�죬��12�춼����30�����֣�����12����ַ�����������Ϊ30����20������д����12������䷢����������������ʾ�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��AB��ֱ����CD������ΪH����P�ǻ�AC�ϵ�һ��(��P����A��C�غ�)������PC��PD��PA��AD����E��AP���ӳ����ϣ�PD��AB���ڵ�F�����������ĸ����ۣ���CH2=AH��BH������AD=��AC����AD2=DF��DP���ܡ�EPC=��APD��
������ȷ�ĸ�����

A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com