
����Ŀ��ij��˾�з���һ��������ߣ��ɱ�Ϊÿ��50Ԫ��Ͷ���г����������ۣ������۵��۲����ڳɱ���������۲��Ź涨�����������ʲ�����70%���г����з��֣���һ��ʱ���ڣ�ÿ����������y�����������۵���x��Ԫ����xΪ����������һ�κ�����ϵ����ͼ��ʾ
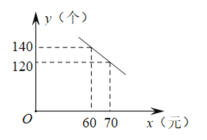
��1�����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2���ù�˾Ҫ��ÿ����3000Ԫ�������������۵���Ӧ��Ϊ����Ԫ��
��3�����۵���Ϊ����Ԫʱ��ÿ���õ����������������Ƕ���Ԫ��
���𰸡���1��y=-2x+260��![]() ������2��80Ԫ����3�����۵���Ϊ85Ԫʱ��ÿ���õ�����������������3150Ԫ
������2��80Ԫ����3�����۵���Ϊ85Ԫʱ��ÿ���õ�����������������3150Ԫ
��������
��1���ɴ���ϵ�����ɵú����Ľ���ʽ��
��2�������������ÿ��������������������з��̿ɽ⣻
��3����ÿ���õ�����ΪwԪ��������ö��κ�����д�ɶ���ʽ������ô𰸣�
�⣺��1����y=kx+b��k��0��bΪ������
���㣨60��140������70��120������ã�
![]() �����
�����![]() ��
��
��y��x�ĺ�����ϵʽΪ��y=-2x+260��
�ⲻ��ʽ��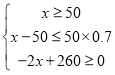 ��
��
�ã�![]() ��xΪ������
��x������
��2��������ã�![]() ��
��
����ã�x2-180x+8000=0��
��ã�x1=80��x2=100��
��![]() =85��
=85��
��x2=100��85�����������⣬��ȥ��
�����۵���Ϊ80Ԫ��
��3����ÿ���õ�����ΪwԪ��������ã�
![]() ��
��
=-2x2+360x-13000
=-2(x-90)2+3200
��a=-2��0�������߿������£�
��w�����ֵ��
��![]() ��
��
�൱x=85ʱ��w���ֵ=3150��
�����۵���Ϊ85Ԫʱ��ÿ���õ�����������������3150Ԫ.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
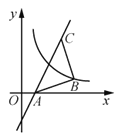
����Ŀ����ͼ������C(3,4)��ֱ��![]() ��
��![]() ���ڵ�A����ABC=90�㣬AB=CB������
���ڵ�A����ABC=90�㣬AB=CB������![]() ����B������A��
����B������A��![]() ��������ƽ��
��������ƽ��![]() ����λ����ǡ�����ڸ������ϣ���
����λ����ǡ�����ڸ������ϣ���![]() ��ֵΪ________��
��ֵΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l��y=��x+4����ֱ��l��ȡ��B1����B1�ֱ���x�ᣬy�������ߣ���x����A1����y����C1��ʹ�ı���OA1B1C1Ϊ�����Σ���ֱ��l��ȡ��B2����B2�ֱ���x�ᣬA1B1�����ߣ���x����A2����A1B1��C2��ʹ�ı���A1A2B2C2Ϊ�����Σ����˷�����ֱ��l��˳��ȡ��B3��B4������Bn��������������A2A3B3C3��A3A4B4C4������An��1AnBnCn����A3������Ϊ___��B5������Ϊ___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
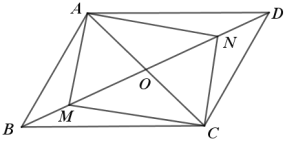
����Ŀ����ͼ����֪ƽ���ı���ABCD��
��1����M��N��BD�����㣬��BM��DN��AC��2OM����֤���ı���AMCN�Ǿ��Σ�
��2������BAD��120�㣬CD��4��AB��AC����ƽ���ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�ı߳�Ϊ3����E��ֱ��CD�ϣ���DE=1������BE����AF��BE�ڵ�H����ֱ��BC�ڵ�F������EF����EF�ij���_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳���Ϊ 1���߶� AB��DE �Ķ˵� A��B��D��E ����С�����εĶ����ϣ�
��1����ͼ�л�һ���� AB Ϊһ���ĵ�����ABC�� ��tan ABC ![]() ����C ��С�����εĶ����ϣ�
����C ��С�����εĶ����ϣ�
��2����ͼ�л�һ���� DE Ϊ�ߵ�ƽ���ı��� DEFG����G 45�� ���� F��G ����С�����εĶ����ϣ����� CG����ֱ��д���߶� CG �ij���
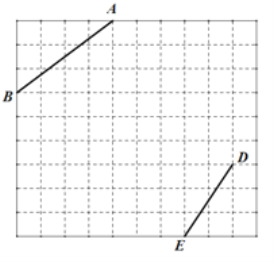
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=��x2+x+6��һ�κ���y=��x+m�����ö��κ�����x���Ϸ���ͼ����x�ᷭ�۵�x���·���ͼ������ಿ�ֲ��䣬�õ�һ���º�������ͼ��ʾ����������ͼ�л��������ͼ��ֱ��y=��x+m����ͼ����4������ʱ��m��ȡֵ��Χ�ǣ�������

A. ��![]() ��m��3 B. ��
��m��3 B. ��![]() ��m��2 C. ��2��m��3 D. ��6��m����2
��m��2 C. ��2��m��3 D. ��6��m����2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Сʢ��������ѧ��������������������ѧ��Ϸ
��1���涨���ĸ����ظ�������ֵС��![]() ����������ͨ���ӷ������������
����������ͨ���ӷ������������![]()
Сʢ��![]() ��������
��������![]() �����Ƿ�����������ʽ���������д����һ�������û�У����˵�����ɣ�
�����Ƿ�����������ʽ���������д����һ�������û�У����˵�����ɣ�
��2���涨���ĸ����ظ�������ֵС![]() ��������ͨ���ӷ����������
��������ͨ���ӷ����������![]()
Сʢ��![]() ��������
��������![]() �������Ҫ����д��һ�������Dz�ͬ����ʽ��
�������Ҫ����д��һ�������Dz�ͬ����ʽ��
��3���ã�2����Сʢ����������ʽ����������ȥ���һ�����У�ʹ���ڵ��ĸ����ĺͶ�����![]() ��Сʢ��
��Сʢ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
![]()
������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
![]()
��![]() ______��
______��![]() _______��������д�������е�ǰ
_______��������д�������е�ǰ![]() ��ĺͣ�
��ĺͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�D��E�ֱ��DZ�AB��AC���е㣬��F��BC��һ�㣬��B����DEF��
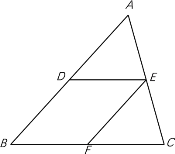
��1����֤���ı���BDEF��ƽ���ı��Σ�
��2��ֱ��д������ABC����ʲô����ʱ���ı���BDEF�����Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com