
【题目】正方形ABCD的边长为3,点E在直线CD上,且DE=1,连接BE,作AF⊥BE于点H,交直线BC于点F,连接EF,则EF的长是_________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
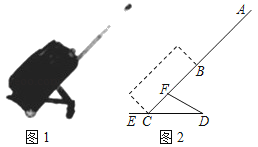
【题目】小红要外出参加一项庆祝活动,需网购一个拉杆箱,图1,图2分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆DE,箱长BC,拉杆AB的长度都相等,B,F在AC上,C在DE上,支杆DF=30cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°,求AC的长度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=3,点D为边AB的中点.点P从点A出发,沿AC方向以每秒1个单位长度的速度向终点C运动,同时点Q从点C出发,以每秒2个单位长度的速度先沿CB方向运动到点B,再沿BA方向向终点A运动,以DP、DQ为邻边构造PEQD,设点P运动的时间为t秒.
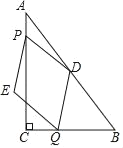
(1)设点Q到边AC的距离为h,直接用含t的代数式表示h;
(2)当点E落在AC边上时,求t的值;
(3)当点Q在边AB上时,设PEQD的面积为S(S>0),求S与t之间的函数关系式;
(4)连接CD,直接写出CD将PEQD分成的两部分图形面积相等时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
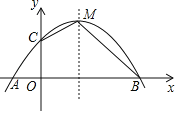
【题目】如图,二次函数y=ax2+bx+4与y轴交于C点,与x轴交于A、B两点,其中A点坐标为(﹣2,0),B点坐标为(8,0).
(1)求经过A,B,C三点的抛物线的解析式;
(2)如果M为抛物线的顶点,连接CM、BM,求四边形COBM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB为直径,BC=CD,过点C作CE⊥AB于点E,CH⊥AD交AD的延长线于点H,连接BD交CE于点G.
(1)求证:CH是⊙O的切线;
(2)若点D为AH的中点,求证:AD=BE;
(3)若sin∠DBA=![]() ,CG=5,求BD的长.
,CG=5,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研发了一款新型玩具,成本为每个50元,投放市场进行试销售.其销售单价不低于成本,按照物价部门规定,销售利润率不高于70%,市场调研发现,在一段时间内,每天销售数量y(个)与销售单价x(元)(x为整数)符合一次函数关系,如图所示
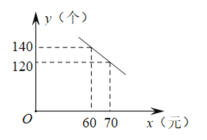
(1)求出y与x的函数关系式,并写出自变量x的取值范围;
(2)该公司要想每天获得3000元的销售利润,销售单价应定为多少元?
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
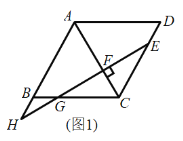
【题目】已知:在菱形 ABCD 中,点 E 是 CD 边上一点,过点 E 作 EF AC 于点 F,交 BC 边于点 G, 交 AB 延长线于点 H.
(1)如图 1,求证:BH=DE;
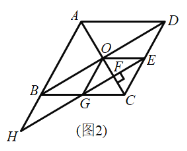
(2)如图 2,当点 E 是 CD 边中点时,连接对角线 BD 交对角线 AC 于点 O,连接 OG、OE,在不添加任何辅助线和字母的情况下,请直接写出图 2 中所有的平行四边形(菱形除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年是全面建成小康社会和“十三五”规划收官之年,为促进销售,某公司开发了A、B两项新产品,销售前景广阔.已知A、B的成本、售价和每日销量如下表所示:
成本(元/件) | 售价(元/件) | 销量(件/日) | |
A | 500 | 700 | 500 |
B | 800 | 1050 | 300 |
根据销售情况,公司对B项产品降价销售,同时对A项产品提价销售,发现B项产品每降价5元就多销售2件,A项产品每提价5元就可少销售1件,要保持每日的总销量不变,设A项产品每天少销售x个,每天总获利为y元.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)要使每天利润不低于208000元,直接写出x的取值范围;
(3)该公司决定每销售一件A产品,就捐给红十字会a(0<a≤100)元作为抗疫基金.当40≤x≤50时,每日的最大利润为237250元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
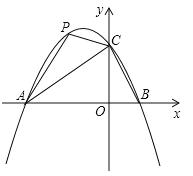
(1)求这个二次函数的关系解析式;
(2)求直线AC的函数解析式;
(3)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com