
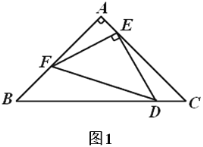
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣬AC��4��BC��3����DΪ��AB���е㣮��P�ӵ�A��������AC������ÿ��1����λ���ȵ��ٶ����յ�C�˶���ͬʱ��Q�ӵ�C��������ÿ��2����λ���ȵ��ٶ�����CB�����˶�����B������BA�������յ�A�˶�����DP��DQΪ�ڱ߹���PEQD�����P�˶���ʱ��Ϊt�룮
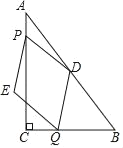
��1�����Q����AC�ľ���Ϊh��ֱ���ú�t�Ĵ���ʽ��ʾh��
��2������E����AC����ʱ����t��ֵ��
��3������Q�ڱ�AB��ʱ����PEQD�����ΪS��S��0������S��t֮��ĺ�����ϵʽ��
��4������CD��ֱ��д��CD��PEQD�ֳɵ�������ͼ��������ʱt��ֵ��
���𰸡���1����0��t��![]() ʱ��h��2t����
ʱ��h��2t����![]() ��t��4ʱ��h��
��t��4ʱ��h��![]() ����2��
����2��![]() ����3����0��t��
����3����0��t��![]() ʱ��
ʱ��![]() ����
����![]() ��t��4ʱ��
��t��4ʱ��![]() ����4��t��ֵΪ
����4��t��ֵΪ![]() ��
��![]() ��
��
��������
��1���ֵ�Q���߶�BC���߶�AB���������ηֱ���⼴�ɣ�
��2������ƽ���ߵȷ��߶ζ���������⼴�ɣ�
��3���ֵ�Q���߶�BD�����߶�AD���������ηֱ���⼴�ɣ�
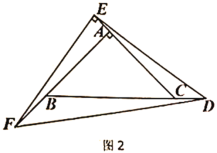
��4������E����ֱ��CD��ʱ��CD��PEQD�ֳɵ�������ͼ�������ȣ����������Σ��ٵ���E��CD�ϣ��ҵ�Q��CB��ʱ ����ͼ3��ʾ�����ڵ���E��CD�ϣ��ҵ�Q��AB��ʱ����ͼ4��ʾ�����ֱ���⼴�ɽ�����⣮
�⣺��1����0��t��![]() ʱ��h��2t��
ʱ��h��2t��
��![]() ��t��4ʱ��h��3��
��t��4ʱ��h��3��![]() ��2t��3����
��2t��3����![]() ��
��
��2������E����AC����ʱ��DQ��AC��
��AD��DB��
��CQ��QB��
��2t��![]() ��
��
��t��![]() ��
��
��3������ͼ1�У���0��t��![]() ʱ����PH��AB��H����PH��PAsinA��
ʱ����PH��AB��H����PH��PAsinA��![]() ��2t��
��2t��
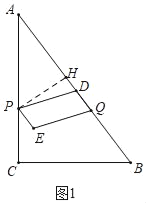
��S��![]() ��
��
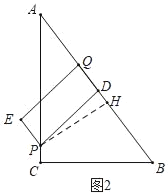
����ͼ2�У���![]() ��t��4ʱ��ͬ���ɵ�
��t��4ʱ��ͬ���ɵ�![]() ��
��
��4������E����ֱ��CD��ʱ��CD��PEQD�ֳɵ�������ͼ�������ȣ����������Σ�
�ٵ���E��CD�ϣ��ҵ�Q��CB��ʱ ����ͼ3��ʾ����
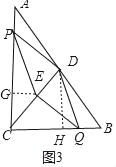
����E��EG��CA�ڵ�G������D��DH��CB�ڵ�H��
��֤Rt��PGE��Rt��DHQ��
��PG��DH��2��
��CG��2��t��GE��HQ��CQ��CH��2t��![]() ��
��
��CD��AD�����DCA����DAC
����Rt��CEG��tan��ECG��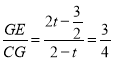 ��
��
��t��![]() ��
��
�ڵ���E��CD�ϣ��ҵ�Q��AB��ʱ����ͼ4��ʾ��������E��EF��CA�ڵ�F��
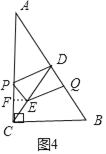
��CD��AD�����CAD����ACD��
��PE��AD�����CPE����CAD����ACD����PE��CE��
��PF��![]() PC��
PC��![]() ��PE��DQ��
��PE��DQ��![]() ��2t��
��2t��
����Rt��PEF��cos��EPF�� ��
��
��t��![]() ��������������Ҫ���t��ֵΪ
��������������Ҫ���t��ֵΪ![]() ��
��![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx��a��0������E��8��0��������ABCD�ı�AB���߶�OE�ϣ���A�ڵ�B����ࣩ����C��D���������ϣ���BAD��ƽ����AM��BC�ڵ�M����N��CD���е㣬��֪OA��2����OA��AD��1��3.
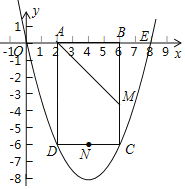
��1���������ߵĽ���ʽ��
��2��F��G�ֱ�Ϊx�ᣬy���ϵĶ��㣬˳������M��N��G��F�����ı���MNGF�����ı���MNGF�ܳ�����Сֵ��
��3����x���·��������������Ƿ���ڵ�P��ʹ��ODP��OD���ϵĸ�Ϊ![]() �������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��4������ABCD������������������ƽ�ƣ���ƽ�ƺ������������εı�����������K��L����ֱ��KLƽ�־��ε����ʱ����������ƽ�Ƶľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ����
����![]() ��ֱ��
��ֱ��![]() ��һ���㣬��
��һ���㣬��![]() ��ֱ��
��ֱ��![]() �϶��㣬��
�϶��㣬��![]() ��ֱ��
��ֱ��![]() ��һ���㣬��
��һ���㣬��![]() ��
��![]() ��
��
��1����ͼ1������![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ��
��![]() ����ʱ�������ж��߶�
����ʱ�������ж��߶�![]() ��
��![]() ��
��![]() ֮����������������ϵ����ֱ��д����Ľ��ۣ�
֮����������������ϵ����ֱ��д����Ľ��ۣ�
��2����ͼ2����![]() ��
��![]() �ӳ����ϣ�
�ӳ����ϣ�![]() ��
��![]() �ӳ����ϣ�
�ӳ����ϣ�![]() ��
��![]() �ӳ�����ʱ����1���еĽ����Ƿ��������������������ͼ2֤�����������������ж��߶�
�ӳ�����ʱ����1���еĽ����Ƿ��������������������ͼ2֤�����������������ж��߶�![]() ��
��![]() ��
��![]() ֮����������������ϵ����֤����Ľ��ۣ�
֮����������������ϵ����֤����Ľ��ۣ�
��3����![]() ����
����![]() ʱ����ֱ��д��
ʱ����ֱ��д��![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB=AC��AD=AE��BD��CE�ཻ�ڵ�O��
��1����֤����ABD�ա�ACE��
��2���жϡ�BOC����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
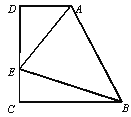
����Ŀ����ͼ��D����ABC�ı�AB��һ�㣬CE��AB��DE��AC�ڵ�F����FA=FC��
��1����֤���ı���ADCE��ƽ���ı��Σ�
��2����AE��EC��EF=EC=5�����ı���ADCE�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l��y=��x+4����ֱ��l��ȡ��B1����B1�ֱ���x�ᣬy�������ߣ���x����A1����y����C1��ʹ�ı���OA1B1C1Ϊ�����Σ���ֱ��l��ȡ��B2����B2�ֱ���x�ᣬA1B1�����ߣ���x����A2����A1B1��C2��ʹ�ı���A1A2B2C2Ϊ�����Σ����˷�����ֱ��l��˳��ȡ��B3��B4������Bn��������������A2A3B3C3��A3A4B4C4������An��1AnBnCn����A3������Ϊ___��B5������Ϊ___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC (BC��AD)����D��90�㣬��ABE��45�㣬BC��CD��
��AE��5��CE=2����BC�ij���Ϊ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�ı߳�Ϊ3����E��ֱ��CD�ϣ���DE=1������BE����AF��BE�ڵ�H����ֱ��BC�ڵ�F������EF����EF�ij���_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������̨����ͬʱ����ֱ��Ϊ![]() �������Ϊ���˽��Ʒ��������������Ա������̨��������������зֱ������ȡ50����Ʒ��������⡢������������������õ�������£���λ��
�������Ϊ���˽��Ʒ��������������Ա������̨��������������зֱ������ȡ50����Ʒ��������⡢������������������õ�������£���λ��![]() ����
����
������ ���� | ƽ���� | ��λ�� | ���� | ���� |
�� | 9.99 | 9.99 | 10.00 | 0.02 |
�� | 9.99 | 10.00 | 10.00 | 0.07 |
�� | 10.02 | 10.01 | 10.00 | 0.02 |
�� | 10.02 | 9.99 | 10.00 | 0.05 |
���������������������ֱ�����ӽ���Ҫ���Ҹ��ȶ��Ļ����ǣ� ��
A.��B.��C.��D.��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com