
【题目】如图,已知AB=AC,AD=AE,BD和CE相交于点O.
(1)求证:△ABD≌△ACE;
(2)判断△BOC的形状,并说明理由.

科目:初中数学 来源: 题型:
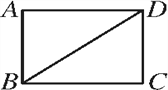
【题目】如图,BD是矩形ABCD的一条对角线.
(1)作BD的垂直平分线EF,分别交AD,BC于点E,F,垂足为点O;(要求用尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)中,连接BE和DF,求证:四边形DEBF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
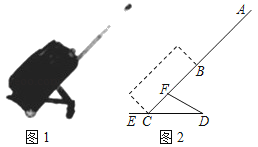
【题目】小红要外出参加一项庆祝活动,需网购一个拉杆箱,图1,图2分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆DE,箱长BC,拉杆AB的长度都相等,B,F在AC上,C在DE上,支杆DF=30cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°,求AC的长度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
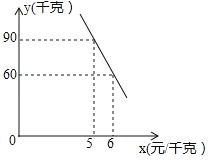
【题目】(12分)某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写如表:

(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
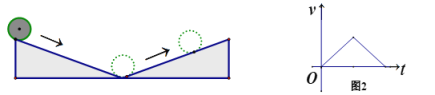
【题目】如图1,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度v(单位:m/s)与运动时间t (单位:s)的函数图象如图2,则该小球的运动路程y(单位:m)与运动时间t(单位:s)之间的函数图象大致是( )
A.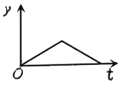 B.
B. C.
C.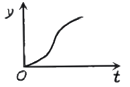 D.
D.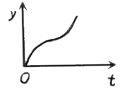
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B为直线y=x上的两点,过A、B两点分别作y轴的平行线交双曲线![]() (x>0)于点C、D两点.若BD=2AC,则4OC2﹣OD2的值为( )
(x>0)于点C、D两点.若BD=2AC,则4OC2﹣OD2的值为( )

A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=3,点D为边AB的中点.点P从点A出发,沿AC方向以每秒1个单位长度的速度向终点C运动,同时点Q从点C出发,以每秒2个单位长度的速度先沿CB方向运动到点B,再沿BA方向向终点A运动,以DP、DQ为邻边构造PEQD,设点P运动的时间为t秒.
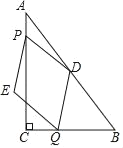
(1)设点Q到边AC的距离为h,直接用含t的代数式表示h;
(2)当点E落在AC边上时,求t的值;
(3)当点Q在边AB上时,设PEQD的面积为S(S>0),求S与t之间的函数关系式;
(4)连接CD,直接写出CD将PEQD分成的两部分图形面积相等时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+4与y轴交于C点,与x轴交于A、B两点,其中A点坐标为(﹣2,0),B点坐标为(8,0).
(1)求经过A,B,C三点的抛物线的解析式;
(2)如果M为抛物线的顶点,连接CM、BM,求四边形COBM的面积.
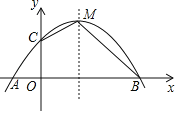
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年是全面建成小康社会和“十三五”规划收官之年,为促进销售,某公司开发了A、B两项新产品,销售前景广阔.已知A、B的成本、售价和每日销量如下表所示:
成本(元/件) | 售价(元/件) | 销量(件/日) | |
A | 500 | 700 | 500 |
B | 800 | 1050 | 300 |
根据销售情况,公司对B项产品降价销售,同时对A项产品提价销售,发现B项产品每降价5元就多销售2件,A项产品每提价5元就可少销售1件,要保持每日的总销量不变,设A项产品每天少销售x个,每天总获利为y元.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)要使每天利润不低于208000元,直接写出x的取值范围;
(3)该公司决定每销售一件A产品,就捐给红十字会a(0<a≤100)元作为抗疫基金.当40≤x≤50时,每日的最大利润为237250元,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com