
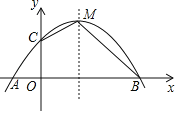
【题目】如图,二次函数y=ax2+bx+4与y轴交于C点,与x轴交于A、B两点,其中A点坐标为(﹣2,0),B点坐标为(8,0).
(1)求经过A,B,C三点的抛物线的解析式;
(2)如果M为抛物线的顶点,连接CM、BM,求四边形COBM的面积.
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
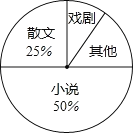
【题目】东营市某学校九年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | n |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | m | 1 |
(1)计算m= ,n= .
(2)在扇形统计图中,“其他”类所在的扇形圆心角为 ;
(3)这个学校共有1000人,则读了戏剧类书籍的学生大约有多少人?
(4)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是乙和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=﹣x+4,在直线l上取点B1,过B1分别向x轴,y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴,A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An﹣1AnBnCn,则A3的坐标为___,B5的坐标为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
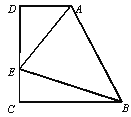
【题目】如图,在四边形ABCD中,AD∥BC (BC>AD),∠D=90°,∠ABE=45°,BC=CD,
若AE=5,CE=2,则BC的长度为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
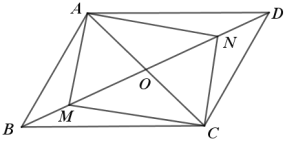
【题目】如图,已知平行四边形ABCD.
(1)若M,N是BD上两点,且BM=DN,AC=2OM,求证:四边形AMCN是矩形;
(2)若∠BAD=120°,CD=4,AB⊥AC,求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,点E在直线CD上,且DE=1,连接BE,作AF⊥BE于点H,交直线BC于点F,连接EF,则EF的长是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )

A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育老师对亮亮和薇薇两名同学的立定跳远进行了五次测试(满分为10分),把他们的成绩绘制成如下统计图.根据图中信息,下列说法正确的是( )
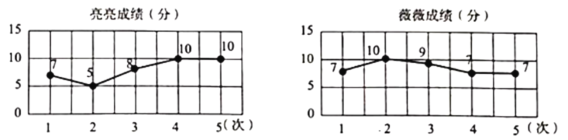
A.亮亮的跳远成绩比薇薇的跳远成绩稳定
B.亮亮的成绩越来越好,如果再跳一次一定还是10分
C.亮亮的第三次成绩与第二次成绩相比,增长率超过![]()
D.亮亮和薇薇的成绩都在8分上下波动,两个人的成绩稳定性一样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com