
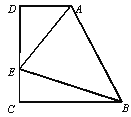
【题目】如图,在四边形ABCD中,AD∥BC (BC>AD),∠D=90°,∠ABE=45°,BC=CD,
若AE=5,CE=2,则BC的长度为_________.
【答案】6
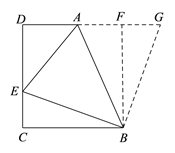
【解析】如下图,过点B作BF⊥DA交DA的延长线于点F,延长AF到G,使FG=CE=2,连接BG,
∴∠BFD=∠BFG=90°,
∵AD∥BC,∠D=90°,
∴∠C=90°,
∵DC=BC,
∴四边形BCDF是正方形,
∴BF=BC,∠CBF=90°,
又∵∠C=∠BFG=90°,CE=FG,
∴△BCE≌△BFG,
∴BF=BG,∠CBE=∠FBG,
∵∠ABE=45°,
∴∠CBE+∠ABF=45°,即∠ABG=45°,
∴∠ABE=∠ABG,
又∵AB=AB,
∴△ABE≌△ABG,
∴AG=AE=5,
∴AF=5-2=3,
设BC=x,则CD=AF=x,
∴DE=x-1,AD=x-3,
∵在Rt△ADE中,DE2+AD2=AE2,
∴![]() ,解得:
,解得:![]() (舍去),
(舍去),
∴BC=6.
故答案为6.


科目:初中数学 来源: 题型:
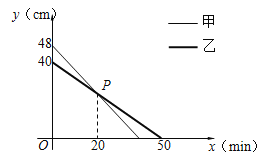
【题目】同时点燃甲乙两根蜡烛,蜡烛燃烧剩下的长度y(cm)与燃烧时间x(min)的关系如图所示.
(1)求点P的坐标,并说明其实际意义;
(2)求点燃多长时间,甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
![]()
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝“春节”,市政府决定在市政广场上增一排灯花,其设计由以下图案逐步演变而成,其中圆圈代表灯花中的灯泡,n代表第n次演变过程,s代表第n次演变后的灯泡的个数,仔细观察下列演变过程,当n=7时,s=( ).
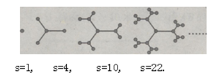
A.162B.176C.190D.214
查看答案和解析>>
科目:初中数学 来源: 题型:
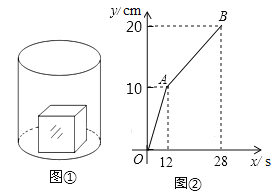
【题目】(2017·吉林)如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
(1)正方体的棱长为 cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活中处处有数学,下列原理运用错误的是![]()
![]() .
.
A.建筑工人砌墙时拉的参照线是运用“两点之间线段最短”的原理
B.修理损坏的椅子腿时斜钉的木条是运用“三角形稳定性”的原理
C.测量跳远的成绩是运用“垂线段最短”的原理
D.将车轮设计为圆形是运用了“圆的旋转对称性”原理
查看答案和解析>>
科目:初中数学 来源: 题型:
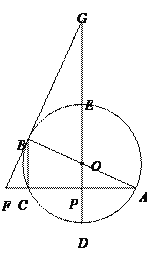
【题目】如图,在半径为3的⊙O中,AB是直径,AC是弦,且AC=4![]() .过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
.过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
(1)求线段AP、CB的长;
(2)若OG=9,求证:FG是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
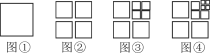
【题目】将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中一个正方形剪开得到图③,图③中共有7个正方形;将图③中一个正方形剪开得到图④,图④中共有10个正方形……如此下去,则第2018个图中共有正方形的个数为( )
 …
…
A.2018个B.6049个C.6052个D.6055个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com