
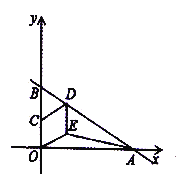
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,
两点,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,四边形
上一点,四边形![]() 是菱形,则
是菱形,则![]() 面积为___________.
面积为___________.
【答案】![]()
【解析】
延长DE交OA于F,如图,先利用一次函数解析式确定B(0,4),A(6![]() ,0),利用三角函数得到∠OBA=60°,接着根据菱形的性质判定△BCD为等边三角形,则∠BCD=∠COE=60°,所以∠EOF=30°,则
,0),利用三角函数得到∠OBA=60°,接着根据菱形的性质判定△BCD为等边三角形,则∠BCD=∠COE=60°,所以∠EOF=30°,则![]() ,然后根据三角形面积公式计算.
,然后根据三角形面积公式计算.
解:延长DE交OA于F,如图,
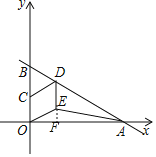
当x=0时,![]() ,则B(0,4),
,则B(0,4),
当y=0时,![]() ,解得x=6
,解得x=6![]() ,则A(6
,则A(6![]() ,0)
,0)
在Rt△AOB中,![]()
∴∠OBA=60°,
∵C是OB的中点,
∴OC=CB=3,
∵四边形OEDC是菱形,
∴CD=BC=DE=CE=3,CD∥OE,
∴△BCD为等边三角形,
∴∠BCD=60°,
∴∠COE=60°,
∴∠EOF=30°,
![]()
△OAE的面积![]()
故答案为: ![]()


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
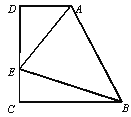
【题目】如图,在四边形ABCD中,AD∥BC (BC>AD),∠D=90°,∠ABE=45°,BC=CD,
若AE=5,CE=2,则BC的长度为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2017秒时点P的坐标是( )
个单位长度,则第2017秒时点P的坐标是( )
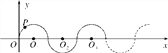
A. (2016,0) B. (2017,1) C. (2017,-1) D. (2018,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
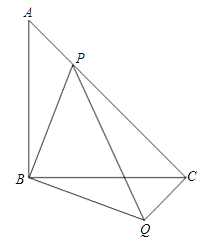
【题目】如图,等腰直角△ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.
(1)求∠PCQ的度数;
(2)当AB=4,AP:PC=1:3时,求PQ的大小;
(3)当点P在线段AC上运动时(P不与A重合),请写出一个反映PA2,PC2,PB2之间关系的等式,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
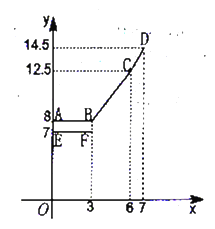
【题目】为缓解油价上涨给出租车行业带来的成本压力,某市拟调整出租车运价,调整方案见下列表格及图象(其中![]() 为常数)
为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过 | 起步价7元 | 起步价 |
超过 | 每公里2元 | 每公里 |
超出 | 每公里 | |
设行驶路程为![]() ,调价前的运价
,调价前的运价![]() (元),调价后运价
(元),调价后运价![]() (元),如图,折线
(元),如图,折线![]() 表示
表示![]() 与
与![]() 之间的函数关系式,线段
之间的函数关系式,线段![]() 表示当
表示当![]() 时,
时,![]() 与
与![]() 的函数关系式,根据图表信息,完成下列各题:
的函数关系式,根据图表信息,完成下列各题:
①填空:![]() ,
,![]() ,
,![]() ;
;
②当![]() 时,求
时,求![]() 与
与![]() 的关系,补充图中该函数的图像;
的关系,补充图中该函数的图像;
③函数![]() 与
与![]() 的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
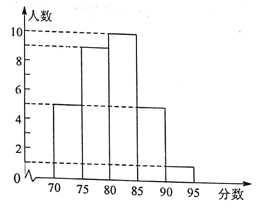
【题目】某学校打算招聘英语教师。对应聘者进行了听、说、读、写的英语水平测试,其中甲、乙两名应聘者的成绩(百分制)如下表所示。

(1)如果学校想招聘说、读能力较强的英语教师,听、说、读、写成绩按照2:4:3:1的比确定,若在甲、乙两人中录取一人,请计算这两名应聘者的平均成绩(百分制)。从他们的成绩看,应该录取谁?
(2)学校按照(1)中的成绩计算方法,将所有应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最后左边一组分数![]() 为:
为:![]() )。
)。
①参加该校本次招聘英语教师的应聘者共有______________人(直接写出答案即可)。
②学校决定由高分到低分录用3名教师,请判断甲、乙两人能否被录用?并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
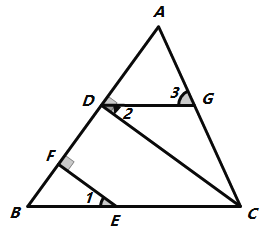
【题目】如图,在△ABC中,CD⊥AB,垂足为D. 点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的理由;
(2)如果∠B=54°,且∠ACD=35°,求的∠3度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:将连续的偶2,4,6,8,…,排成如表:
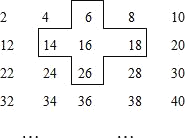
(1)请你求出十字框中的五个数的和;
(2)设中间的数为x,请你用含x的式子表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五个数,这五个数的和能等于2018吗?如能,写出这五个数,如不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com