
【题目】如图,等腰直角△ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.
(1)求∠PCQ的度数;
(2)当AB=4,AP:PC=1:3时,求PQ的大小;
(3)当点P在线段AC上运动时(P不与A重合),请写出一个反映PA2,PC2,PB2之间关系的等式,并加以证明.
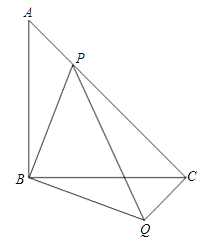
【答案】(1)90°;(2)2![]() ;(3)2PB2=PA2+PC2.
;(3)2PB2=PA2+PC2.
【解析】
(1)由于∠PCB=∠BCQ=45°,故有∠PCQ=90°.
(2)由等腰直角三角形的性质知,AC=4![]() ,根据已知条件,可求得AP,PC的值,再由勾股定理求得PQ的值.
,根据已知条件,可求得AP,PC的值,再由勾股定理求得PQ的值.
(3)由于△PBQ也是等腰直角三角形,故有PQ2=2PB2=PA2+PC2.
(1)由题意知,△ABP≌△CQB,
∴∠A=∠ACB=∠BCQ=45°,∠ABP=∠CPQ,AP=CQ,PB=BQ,
∴∠PCQ=∠ACB+∠BCQ=90°,∠ABP+∠PBC=∠CPQ+∠PBC=90°,
∴△BPQ是等腰直角三角形,△PCQ是直角三角形.
(2)当AB=4,AP:PC=1:3时,有AC=4![]() ,AP=
,AP=![]() ,PC=3
,PC=3![]() ,
,
∴PQ=![]() =2
=2![]() .
.
(3)存在2PB2=PA2+PC2,由于△BPQ是等腰直角三角形,
∴PQ=![]() PB.
PB.
∵AP=CQ,∴PQ2=PC2+CQ2=PA2+PC2,
故有2PB2=PA2+PC2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为庆祝“春节”,市政府决定在市政广场上增一排灯花,其设计由以下图案逐步演变而成,其中圆圈代表灯花中的灯泡,n代表第n次演变过程,s代表第n次演变后的灯泡的个数,仔细观察下列演变过程,当n=7时,s=( ).
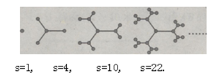
A.162B.176C.190D.214
查看答案和解析>>
科目:初中数学 来源: 题型:
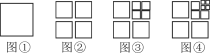
【题目】将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中一个正方形剪开得到图③,图③中共有7个正方形;将图③中一个正方形剪开得到图④,图④中共有10个正方形……如此下去,则第2018个图中共有正方形的个数为( )
 …
…
A.2018个B.6049个C.6052个D.6055个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张第一次用180元购买了8套儿童服装,以一定价格出售.如果以每套儿童服装80元的价格为标准,超出的记作整数,不足的记作负数,记录如下(单位:元):
![]()
请通过计算说明:
(1)小张卖完这8套儿童服装后是盈利还是亏损?盈利(或亏损)了多少钱?
(2)每套儿童服装的平均售价是多少元?
(3)小张第二次用第一次的进价再次购买900元的儿童服装,如果他预计第二次每套服装的平均售价75元,按他的预计第二次售价可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
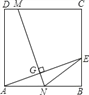
【题目】如图,ABCD为正方形,E为BC上一点,将正方形折叠,使A点与E点重合,折痕为MN,若tan∠AEN=![]() ,DC+CE=10.
,DC+CE=10.
(1)求△ANE的面积;
(2)求sin∠ENB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
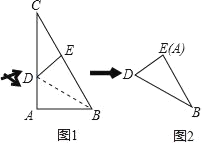
【题目】在三角形纸片ABC中,∠A=90°,∠C=30°,AC=10cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),剪去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为_____cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com