
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
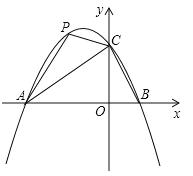
(1)求这个二次函数的关系解析式;
(2)求直线AC的函数解析式;
(3)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+2;(2)
x+2;(2)![]() ;(3)存在,(
;(3)存在,(![]() )
)
【解析】
(1)直接用待定系数法即可解答;
(2)先确定C点坐标,设直线AC的函数解析式y=kx+b,最后用待定系数法求解即可;
(3)连接PO,作PM⊥x轴于M,PN⊥y轴于N,然后求出△ACP面积的表达式,最后利用二次函数的性质求最值即可.
解:(1)∵抛物线y=ax2+bx+2过点A(﹣3,0),B(1,0),
∴![]()
解得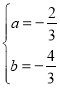 ,
,
∴二次函数的关系解析式为y=﹣![]() x2﹣
x2﹣![]() x+2;
x+2;
(2)∵当x=0时,y=2,
∴C(0,2)
设直线AC的解析式为![]() ,把A、C两点代入得
,把A、C两点代入得
![]() 解得
解得![]()
∴直线AC的函数解析式为![]() ;
;
(3)存在.
如图: 连接PO,作PM⊥x轴于M,PN⊥y轴于N
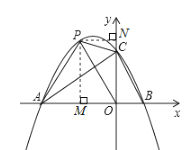
设点P坐标为(m,n),则n=![]() ),PN=-m,AO=3
),PN=-m,AO=3
当x=0时,y=![]() =2,
=2,
∴点C的坐标为(0,2),OC=2
∵![]()
![]()
=![]()
∵a=-1<0
∴函数S△PAC=-m2-3m有最大值
∴b当m=![]()
∴当m=![]() 时,S△PAC有最大值n=
时,S△PAC有最大值n=![]()
∴当△ACP的面积最大时,P的坐标为(![]() ).
).


科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,点E在直线CD上,且DE=1,连接BE,作AF⊥BE于点H,交直线BC于点F,连接EF,则EF的长是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂的四台机床同时生产直径为![]() 的零件,为了了解产品质量,质量检验员从这四台机床生产的零件中分别随机抽取50件产品,经过检测、整理、描述与分析,得到结果如下(单位:
的零件,为了了解产品质量,质量检验员从这四台机床生产的零件中分别随机抽取50件产品,经过检测、整理、描述与分析,得到结果如下(单位:![]() ):
):
特征数 机床 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 9.99 | 9.99 | 10.00 | 0.02 |
乙 | 9.99 | 10.00 | 10.00 | 0.07 |
丙 | 10.02 | 10.01 | 10.00 | 0.02 |
丁 | 10.02 | 9.99 | 10.00 | 0.05 |
从样本来看,生产的零件直径更接近标准要求且更稳定的机床是( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育老师对亮亮和薇薇两名同学的立定跳远进行了五次测试(满分为10分),把他们的成绩绘制成如下统计图.根据图中信息,下列说法正确的是( )
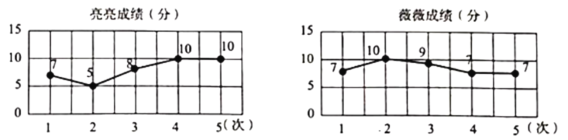
A.亮亮的跳远成绩比薇薇的跳远成绩稳定
B.亮亮的成绩越来越好,如果再跳一次一定还是10分
C.亮亮的第三次成绩与第二次成绩相比,增长率超过![]()
D.亮亮和薇薇的成绩都在8分上下波动,两个人的成绩稳定性一样
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,扇形![]() 的半径为3,面积为
的半径为3,面积为![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
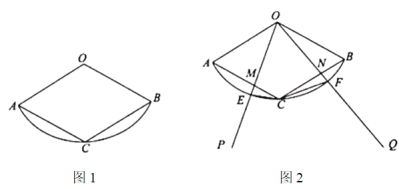
(1)求证:四边形![]() 是菱形;
是菱形;
(2)如图2,![]() ,
,![]() 绕点
绕点![]() 旋转,与
旋转,与![]() ,
,![]() 分别交于点
分别交于点![]() (点
(点![]() 与点
与点![]() 均不重合),与
均不重合),与![]() 交于
交于![]() 两点.
两点.
①求![]() 的值;
的值;
②如图2,连接![]() ,
,![]() ,若
,若![]() 的度数是定值,则直接写出
的度数是定值,则直接写出![]() 的度数;若不是,请说明理由.
的度数;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E分别是边AB、AC的中点,点F是BC上一点,∠B=∠DEF.
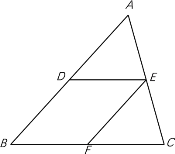
(1)求证:四边形BDEF是平行四边形;
(2)直接写出当△ABC满足什么条件时,四边形BDEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,汽车以速度V(m/s)匀速行驶,若一路绿灯通过路口A、B、C、D且10≤V≤25,则称V为绿灯速度.已知各路口红灯、绿灯均每隔30 s交替一次,其余因素忽略不计.

(图1)
I.从红绿灯设置到绿灯速度
设汽车在第0秒出发,行驶t s后路程为S m.图2表示在某种红绿灯设置下汽车行驶的情况.
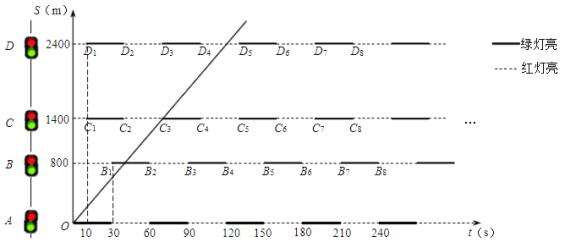
(图2)
(1)路段BC的长度为______m,路口A绿灯亮起______s后路口D绿灯亮起;
(2)求出射线OC3所对应的V的值,判断此时V是否为绿灯速度,并说明理由;
(3)写出这种红绿灯设置下绿灯速度的取值范围,并在图2中画出对应的示意图
II.从绿灯速度到红绿灯设置
(4)当V=20时,汽车经过的每个路口绿灯都恰好开始亮起.根据题意,在图3中画图表示各路口的红绿灯设置.
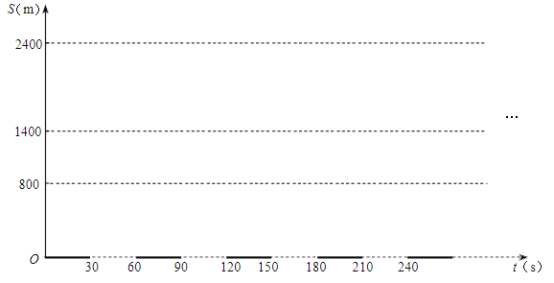 (图3)
(图3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (a≠0)的图象如图所示,
(a≠0)的图象如图所示,
有下列结论:
①a、b同号;
②当x=1和x=3时,函数值相等;
③4a+b=0;
④当-1<x<5时,y<0.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】魔术师说将你想到的数进行以下四步操作,我就可以猜到你心里想的数.
第一步:心中想一个数,求其平方;
第二步:想比这个数小2的数,求其平方;
第三步:求其平方的差值;
第四步:平方的差值除以4再加1.
将结果告诉我,我就能猜中你心里想的数.
(1)若你想的数是5,求出你告诉魔术师的结果是多少.
(2)聪明的同学们,你觉得魔术师的步骤一定能猜中你心中的数吗?请用代数式计算证明你的结论.
解答:魔术师 猜中你心中的数(填“能”或“否”);
证明:设心中想的数为![]() (
(![]() 为任意实数)
为任意实数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com