
【题目】如图1,扇形![]() 的半径为3,面积为
的半径为3,面积为![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
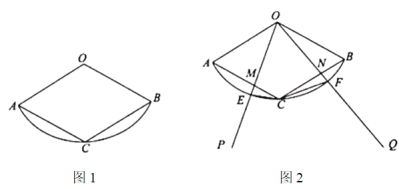
(1)求证:四边形![]() 是菱形;
是菱形;
(2)如图2,![]() ,
,![]() 绕点
绕点![]() 旋转,与
旋转,与![]() ,
,![]() 分别交于点
分别交于点![]() (点
(点![]() 与点
与点![]() 均不重合),与
均不重合),与![]() 交于
交于![]() 两点.
两点.
①求![]() 的值;
的值;
②如图2,连接![]() ,
,![]() ,若
,若![]() 的度数是定值,则直接写出
的度数是定值,则直接写出![]() 的度数;若不是,请说明理由.
的度数;若不是,请说明理由.
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB为直径,BC=CD,过点C作CE⊥AB于点E,CH⊥AD交AD的延长线于点H,连接BD交CE于点G.
(1)求证:CH是⊙O的切线;
(2)若点D为AH的中点,求证:AD=BE;
(3)若sin∠DBA=![]() ,CG=5,求BD的长.
,CG=5,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完全平方公式是初中数学的重要公式之一:![]() ,完全平方公式既可以用来进行整式计算又可以用来进行分解因式,在学习中芳芳同学发现
,完全平方公式既可以用来进行整式计算又可以用来进行分解因式,在学习中芳芳同学发现![]() 也可以用完全平方公式进行分解因式,
也可以用完全平方公式进行分解因式,![]() ;根据以上发现解决问题
;根据以上发现解决问题
(1)写出一个上面相同的式子,并进行分解因式;
(2)若![]() ,请用
,请用![]() ,
,![]() 表示
表示![]() ,
,![]()
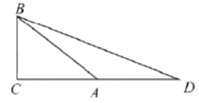
(3)如图在![]() 中,
中,![]() ,
,![]() ,
,![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,求
,求![]() 的长(参考上面提供的方法把结果进行化简)
的长(参考上面提供的方法把结果进行化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
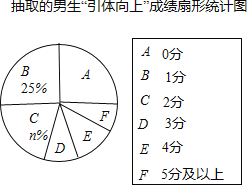
【题目】某市明年的初中毕业升学考试,拟将“引体向上”作为男生体育考试的一个必考项目,满分为10分.有关部门为提前了解明年参加初中毕业升学考试的男生的“引体向上”水平,在全市八年级男生中随机抽取了部分男生,对他们的“引体向上”水平进行测试,并将测试结果绘制成如下统计图表(部分信息未给出):
请你根据统计图表中的信息,解答下列问题:
抽取的男生“引体向上”成绩统计表
成绩 | 人数 |
0分 | 32 |
1分 | 30 |
2分 | 24 |
3分 | 11 |
4分 | 15 |
5分及以上 | m |
(1)填空:m= ,n= .
(2)求扇形统计图中D组的扇形圆心角的度数;
(3)目前该市八年级有男生3600名,请估计其中“引体向上”得零分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
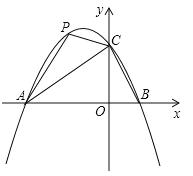
(1)求这个二次函数的关系解析式;
(2)求直线AC的函数解析式;
(3)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲盒中有标号为1、2、4的牌子,乙盒中有标号为1、2、3、4的牌子,两个盒子均不透明,这些牌子除标号外无其他差别.小勇从甲盒中随机摸出一个牌子,标号为a,小婷从乙盒中随机摸出一个牌子,标号为b,若a<b,则小勇获胜;若a≥b,则小婷获胜.

(1)求小勇获胜的概率;
(2)若小勇摸出的牌子标号为2,在不知道小婷标号的情况下,他获胜的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
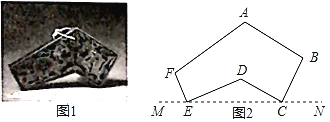
【题目】磐是我国国带的一种打击乐器和礼器(如图),据先秦文献《吕氏春秋古乐篇》记载:尧命击磐“以象上帝”“以致舞百兽”,描绘出一幅古老的原始社会的乐舞生活场景.20世纪70年代在山西夏县出土了一件大石磐,上部有一穿孔,击之声音悦耳,经测定,此磐据经约4000年,属于夏代的遗存,这是迄今发现最早的磐的实物.从正面看磐是一个多边形图案(如图2),已知MN为地面,测得AB=30厘米,BC=20厘米,∠BCN=60°,∠ABC=95°,求磐的最高点A到地面MN的高度h.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,![]() ≈1.73,结果保留一位小数)
≈1.73,结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F.
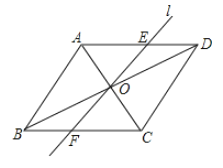
(1)求证:△AOE≌△COF;
(2)当α=30°时,求线段EF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com