
【题目】如图,四边形ABCD内接于⊙O,AB为直径,BC=CD,过点C作CE⊥AB于点E,CH⊥AD交AD的延长线于点H,连接BD交CE于点G.
(1)求证:CH是⊙O的切线;
(2)若点D为AH的中点,求证:AD=BE;
(3)若sin∠DBA=![]() ,CG=5,求BD的长.
,CG=5,求BD的长.

【答案】(1)见解析;(2)见解析;(3)16
【解析】
(1)连接OC,OD,证得∠BAH=∠BOC,得出AH∥OC,则OC⊥CH,则结论得证;
(2)连接AC,得出CE=CH,证明Rt△CEB≌Rt△CHD(HL),则BE=DH,证出AD=DH,则可得出结论;
(3)延长CE交⊙O于点F,得出GB=GC=5,在Rt△GEB中,sin∠GBE=![]() ,可求出GE=3,由勾股定理求出BE,证明Rt△AEC∽△Rt△CEB,由
,可求出GE=3,由勾股定理求出BE,证明Rt△AEC∽△Rt△CEB,由![]() 可求出AE,再求出AD,则可得出BD的长.
可求出AE,再求出AD,则可得出BD的长.
(1)证明:如图,连接OC,OD,
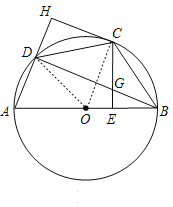
∵BC=CD,
∴∠BOC=∠COD=![]() ∠BOD,
∠BOD,
又∵∠BAH=![]() ∠BOD,
∠BOD,
∴∠BAH=∠BOC,
∴AH∥OC,
∵AH⊥CH,
∴OC⊥CH,
∴CH是⊙O的切线;
(2)证明:如图,连接AC,
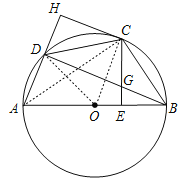
∵BC=CD,
∴![]() ,
,
∴∠BAC=∠CAH,
又∵CE⊥AB,CH⊥AH,
∴CE=CH,
∴Rt△CEB≌Rt△CHD(HL),
∴BE=DH,
∵点D为AH的中点,
∴AD=DH,
∴AD=BE;
(3)解:如图,延长CE交⊙O于点F,
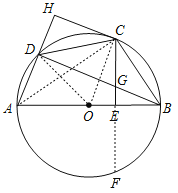
∵AB是⊙O的直径,CF⊥AB,
∴![]() =
=![]() =
=![]() ,
,
∴∠BCE=∠CBD,
∴GB=GC=5,
在Rt△GEB中,sin∠GBE=![]() ,
,
∴GE=3,
∴BE=![]() =
=![]() =4,
=4,
CE=CG+GE=5+3=8,
∵∠EAC=∠CAD=∠CBD=∠BCE,∠AEC=∠CEB=90°,
∴Rt△AEC∽△Rt△CEB,
∴![]() ,
,
即![]() ,
,
∴AE=16,
∴AB=AE+BE=16+4=20,
在Rt△ADB中,sin∠DBA=![]() ,
,
∴AD=![]() AB=
AB=![]() ×20=12,
×20=12,
∴BD=![]() =
=![]() =16.
=16.


科目:初中数学 来源: 题型:
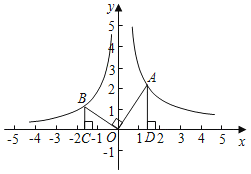
【题目】如图,第一象限内的点A在反比例函数y=![]() 上,第二象限的点B在反比例函数y=
上,第二象限的点B在反比例函数y=![]() 上,且OA⊥OB,
上,且OA⊥OB,![]() ,BC、AD垂直于x轴于C、D,则k的值为_____.
,BC、AD垂直于x轴于C、D,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=5,求四边形ADCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
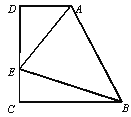
【题目】如图,在四边形ABCD中,AD∥BC (BC>AD),∠D=90°,∠ABE=45°,BC=CD,
若AE=5,CE=2,则BC的长度为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
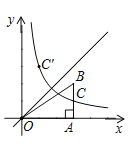
【题目】如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于点A,反比例函数y=![]() (x>0)的图象与线段AB相交于点C,C是线段AB的中点,点C关于直线y=x的对称点C'的坐标为(m,6)(m≠6),若△OAB的面积为12,则k的值为( )
(x>0)的图象与线段AB相交于点C,C是线段AB的中点,点C关于直线y=x的对称点C'的坐标为(m,6)(m≠6),若△OAB的面积为12,则k的值为( )
A.4B.6C.8D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,点E在直线CD上,且DE=1,连接BE,作AF⊥BE于点H,交直线BC于点F,连接EF,则EF的长是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,扇形![]() 的半径为3,面积为
的半径为3,面积为![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
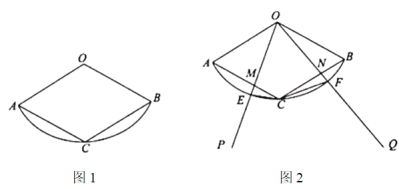
(1)求证:四边形![]() 是菱形;
是菱形;
(2)如图2,![]() ,
,![]() 绕点
绕点![]() 旋转,与
旋转,与![]() ,
,![]() 分别交于点
分别交于点![]() (点
(点![]() 与点
与点![]() 均不重合),与
均不重合),与![]() 交于
交于![]() 两点.
两点.
①求![]() 的值;
的值;
②如图2,连接![]() ,
,![]() ,若
,若![]() 的度数是定值,则直接写出
的度数是定值,则直接写出![]() 的度数;若不是,请说明理由.
的度数;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com