
【题目】如图,△ABC中,D、E分别是边AB、AC的中点,点F是BC上一点,∠B=∠DEF.
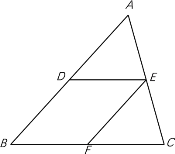
(1)求证:四边形BDEF是平行四边形;
(2)直接写出当△ABC满足什么条件时,四边形BDEF是菱形.
【答案】(1)见解析;(2)答案不唯一,如AB=BC.
【解析】
(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC,然后证明DB∥EF,根据两组对边分别平行的四边形是平行四边形证明;
(2)根据邻边相等的平行四边形是菱形,得出BD=BF,推出AB=BC即可.
(1)∵ 点D、E分别是边AB、AC的中点,
∴ DE是△ABC的中位线.
∴ DE∥BC.
∴ ∠B=∠ADE.
又 ∠B=∠DEF.
∴ ∠ADE=∠DEF.
∴ BD∥EF.
∵ DE∥BC,BD∥EF,
∴ 四边形BDEF是平行四边形.
(2)答案不唯一,如AB=BC.
∵ DE是△ABC的中位线
∴BD=![]() AB ,BF=
AB ,BF= ![]() BC
BC
∵ AB=BC
∴BD=BF
∴![]() BDEF是菱形
BDEF是菱形


科目:初中数学 来源: 题型:
【题目】某公司研发了一款新型玩具,成本为每个50元,投放市场进行试销售.其销售单价不低于成本,按照物价部门规定,销售利润率不高于70%,市场调研发现,在一段时间内,每天销售数量y(个)与销售单价x(元)(x为整数)符合一次函数关系,如图所示
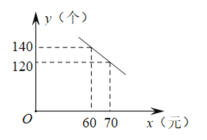
(1)求出y与x的函数关系式,并写出自变量x的取值范围;
(2)该公司要想每天获得3000元的销售利润,销售单价应定为多少元?
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过多方努力,北京市2019年在区域空气质量同步改善、气象条件较常年整体有利的情况下,大气环境中细颗粒物(![]() )等四项主要污染物同比均明显改善对北京市空气质量的有关数据进行收集、整理、描述与分析,下面给出了部分信息:
)等四项主要污染物同比均明显改善对北京市空气质量的有关数据进行收集、整理、描述与分析,下面给出了部分信息:
a.北京市2019年空气质量各级别分布情况如下图(全年无严重污染日)(不完整):

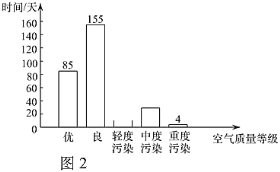
b.北京市2019年大气环境中二氧化硫(![]() )的年均浓度为4微克/立方米,稳定达到国家二级标准(60微克/立方米);
)的年均浓度为4微克/立方米,稳定达到国家二级标准(60微克/立方米);![]() ,二氧化氮(
,二氧化氮(![]() )的年均浓度分别为68微克/立方米,37微克/立方米,均首次达到国家二级标准(70微克/立方米,40微克/立方米);
)的年均浓度分别为68微克/立方米,37微克/立方米,均首次达到国家二级标准(70微克/立方米,40微克/立方米);![]() 的年均浓度为
的年均浓度为![]() 微克立方米,仍是北京市大气主要污染物,超过国家二级标准(35微克/立方米)的20%.
微克立方米,仍是北京市大气主要污染物,超过国家二级标准(35微克/立方米)的20%.
c.北京市2019年大气环境中![]() 月均浓度变化情况如下:
月均浓度变化情况如下:
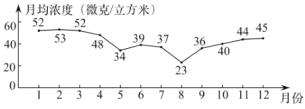
二氧化硫(![]() )月均浓度(单位:微克/立方米)如下(不完整):
)月均浓度(单位:微克/立方米)如下(不完整):
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
月均浓度 | 9 | 6 | 5 | 4 | 3 | 2 | 3 | 3 | 5 | 4 |
(以上数据来源于北京市生态环境局官方网站)
根据以上信,回答下列问题:
(1)北京市2019年空气质量为“轻度污染”天数为( ).
A.82 B.92 C.102
(2)![]() 的值是______;
的值是______;
(3)北京市2019年大气环境中![]() 月均浓度达到国家二级标准的概率为______;
月均浓度达到国家二级标准的概率为______;
(4)北京市2019年大气环境中![]() 月均浓度的众数是4,则中位数是______.
月均浓度的众数是4,则中位数是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年在2月27日国务院对外新闻发布会上,中国疾控中心发言人提到:“在新冠肺炎低风险区域出行仍需戴口罩.”某单位复工,采购了一批医用外科口罩,单价分别为1元、1.5元、3元、5元、10元,每天随机配发给每位在岗员工一个口罩.现将连续10天口罩配发量的情况制成如下统计表.
配发量/个 | 30 | 25 | 20 | 15 |
天数/天 | 2 |
|
| 1 |
已知配发量的平均数是23个,中位数是![]() 个,众数是
个,众数是![]() 个.
个.
(1)求![]() 的值,并计算
的值,并计算![]() ;
;
(2)将配发15个口罩那一天中不同型号的口罩发放情况进行统计,绘制成如图所示的尚不完整的统计图.补全统计图,并求小李当天获得不低于3元口罩的概率;
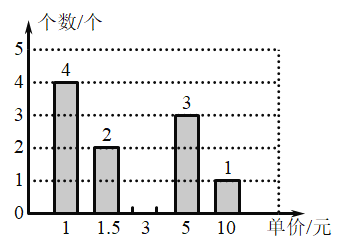
(3)若继续发放两天口罩,且这12天口罩配发量的众数与前10天口罩配发量的众数不同(例如:只要在第11天,第12天都发放30个口罩,则这12天口罩发放量的众数为30个和20个),写出这12天口罩配发量的众数(括号内示例情况不必再述).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
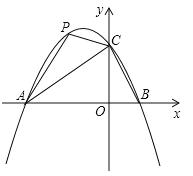
(1)求这个二次函数的关系解析式;
(2)求直线AC的函数解析式;
(3)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2-6ax+5a(a为常数)的图像为抛物线C.
(1)求证:不论a为何值,抛物线C与x轴总有两个不同的公共点;
(2)设抛物线C交x轴于点A、B,交y轴于点D,若△ABD的面积为20,求a的值;
(3)设点E(2,4)、F(3,4),若抛物线C与线段EF只有一个公共点,结合函数图像,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为贯彻落实“绿水青山就是金山银山“的发展理念,投资组建了日废水处理量为m吨的废水处理车间,对该厂工业废水进行无害化处理. 但随着工厂生产规模的扩大,该车间经常无法完成当天工业废水的处理任务,需要将超出日废水处理量的废水交给第三方企业处理. 已知该车间处理废水,每天需固定成本30元,并且每处理一吨废水还需其他费用8元;将废水交给第三方企业处理,每吨需支付12元.根据记录,5月21日,该厂产生工业废水35吨,共花费废水处理费370元.
(1)求该车间的日废水处理量m;
(2)为实现可持续发展,走绿色发展之路,工厂合理控制了生产规模,使得每天废水处理的平均费用不超过10元/吨,试计算该厂一天产生的工业废水量的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB垂直于弦CD,垂足为H,点P是弧AC上的一点(点P不与A,C重合),连结PC,PD,PA,AD,点E在AP的延长线上,PD与AB交于点F.给出下列四个结论:①CH2=AH·BH;②弧AD=弧AC;③AD2=DF·DP;④∠EPC=∠APD.
其中正确的个数有

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线:![]() ,与
,与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() :
:![]() ,经过点
,经过点![]() ,且与
,且与![]() 轴的另一个交点为点
轴的另一个交点为点![]() .
.

(1)若![]() ,求此时抛物线的解析式、顶点坐标及点
,求此时抛物线的解析式、顶点坐标及点![]() 坐标;
坐标;
(2)在直线![]() 与抛物线
与抛物线![]() 围成的封闭图形边界上,横、纵坐标均为整数的点称为“神秘点”,求出在(l)的条件下“神秘点”的个数;
围成的封闭图形边界上,横、纵坐标均为整数的点称为“神秘点”,求出在(l)的条件下“神秘点”的个数;
(3)①直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标会变吗?说明理由;
的坐标会变吗?说明理由;
②若抛物线![]() 与直线
与直线![]() 在
在![]() 的范围内有唯一公共点,请直接写出
的范围内有唯一公共点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com