
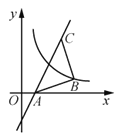
【题目】如图,过点C(3,4)的直线![]() 交
交![]() 轴于点A,∠ABC=90°,AB=CB,曲线
轴于点A,∠ABC=90°,AB=CB,曲线![]() 过点B,将点A沿
过点B,将点A沿![]() 轴正方向平移
轴正方向平移![]() 个单位长度恰好落在该曲线上,则
个单位长度恰好落在该曲线上,则![]() 的值为________.
的值为________.
【答案】4
【解析】
分别过点B、点C作![]() 轴和
轴和![]() 轴的平行线,两条平行线相交于点M,与
轴的平行线,两条平行线相交于点M,与![]() 轴的交点为N.将C(3,4)代入
轴的交点为N.将C(3,4)代入![]() 可得b=-2,然后求得A点坐标为(1,0),证明△ABN≌△BCM,可得AN=BM=3,CM=BN=1,可求出B(4,1),即可求出k=4,由A点向上平移后落在
可得b=-2,然后求得A点坐标为(1,0),证明△ABN≌△BCM,可得AN=BM=3,CM=BN=1,可求出B(4,1),即可求出k=4,由A点向上平移后落在![]() 上,即可求得a的值.
上,即可求得a的值.
分别过点B、点C作![]() 轴和
轴和![]() 轴的平行线,两条平行线相交于点M,与
轴的平行线,两条平行线相交于点M,与![]() 轴的交点为N,则∠M=∠ANB=90°,
轴的交点为N,则∠M=∠ANB=90°,
把C(3,4)代入![]() ,得4=6+b,解得:b=-2,
,得4=6+b,解得:b=-2,
所以y=2x-2,
令y=0,则0=2x-2,解得:x=1,
所以A(1,0),
∵∠ABC=90°,
∴∠CBM+∠ABN=90°,
∵∠ANB=90°,
∴∠BAN+∠ABN=90°,
∴∠CBM=∠BAN,
又∵∠M=∠ANB=90°,AB=BC,
∴△ABN≌△BCM,
∴AN=BM,BN=CM,
∵C(3,4),∴设AN=m,CM=n,
则有![]() ,解得
,解得![]() ,
,
∴ON=3+1=4,BN=1,
∴B(4,1),
∵曲线![]() 过点B,
过点B,
∴k=4,
∴![]() ,
,
∵将点A沿![]() 轴正方向平移
轴正方向平移![]() 个单位长度恰好落在该曲线上,此时点A移动后对应点的坐标为(1,a),
个单位长度恰好落在该曲线上,此时点A移动后对应点的坐标为(1,a),
∴a=4,
故答案为:4.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=60°,BC=2,CD是△ABC的一条高线.若E,F分别是CD和BC上的动点,则BE+EF的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,![]() 、
、![]() 是
是![]() 的中线,
的中线,![]() 于点
于点![]() ,像
,像![]() 这样的三角形均称为“中垂三角形”.
这样的三角形均称为“中垂三角形”.
(特例探究)
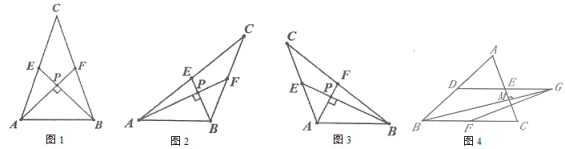
(1)如图1,当![]() ,
,![]() 时,
时,![]() _____,
_____,![]() ______;
______;
如图2,当![]() ,
,![]() 时,
时,![]() _____,
_____,![]() ______;
______;
(归纳证明)
(2)请你观察(1)中的计算结果,猜想![]() 、
、![]() 、
、![]() 三者之间的关系,用等式表示出来,并利用图3证明你的结论;
三者之间的关系,用等式表示出来,并利用图3证明你的结论;
(拓展证明)
(3)如图4,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]()
![]() 的中点,连结
的中点,连结![]() 并延长至
并延长至![]() ,使得
,使得![]() ,连结
,连结![]() ,当
,当![]() 于点
于点![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,△ABC的三个顶点坐标分别为A(2,1),B(1,4),C(3,2).请解答下列问题:
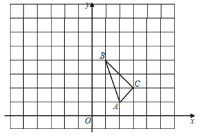
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点的坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的右侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点的坐标;
(3)如果点D(a,b)在线段BC上,请直接写出经过(2)的变化后对应点D2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建文明城市,增强学生的环保意识.随机抽取8名学生,对他们的垃圾分类投放情况进行调查,这8名学生分别标记为![]() ,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
学生 垃圾类别 |
|
|
|
|
|
|
|
|
厨余垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
可回收垃圾 | √ | × | √ | × | × | √ | √ | √ |
有害垃圾 | × | √ | × | √ | √ | × | × | √ |
其他垃圾 | × | √ | √ | × | × | √ | √ | √ |
(1)求8名学生中至少有三类垃圾投放正确的概率;
(2)为进一步了解垃圾分类投放情况,现从8名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访,试用标记的字母列举所有可能抽取的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 边形,甲、乙、丙三位同学有以下三种说法:
边形,甲、乙、丙三位同学有以下三种说法:
甲:五边形的内角和为![]()
乙:正六边形每个内角为![]()
丙:七边形共有对角线14条
(1)判断三种说法是否正确,并对其中你认为不对的说法用计算进行说明
(2)若![]() 边形的对角线共35条,求该
边形的对角线共35条,求该![]() 边形的内角和
边形的内角和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D、E分别在边AB、BC上,AD=BE,CD与AE交于F.

(1)求∠AFD的度数;
(2)若BE=m,CE=n.
①求![]() 的值;(用含有m和n的式子表示)
的值;(用含有m和n的式子表示)
②若![]() =
=![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com