
如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为D,直线AC交⊙C于点E、F,且CF= AC.
AC.
(1)求∠ACB的度数;
(2)若AC=8,求△ABF的面积.

(1)∠ACB=120°.
(2)24
【解析】
试题分析:(1)连接DC,由AB是⊙C的切线,可知CD⊥AB,根据CD= AC,得出∠A=30°,又AC=BC,从而可求得∠ACB的度数.
AC,得出∠A=30°,又AC=BC,从而可求得∠ACB的度数.
(2)由(1)可得∠ACD=∠BCD=∠BCF,从而可得△ACD≌△BCF,求得∠AFB=90°,已知AC=8,根据已知求得AF=12,由于∠A=30°得出BF= AB,由勾股定理求得BF的长,从而可求得三角形的面积.
AB,由勾股定理求得BF的长,从而可求得三角形的面积.
试题解析:(1)连接CD,

∵AB是⊙C的切线,
∴CD⊥AB,
∵CF= AC,CF=CE,
AC,CF=CE,
∴AE=CE,
∴ED= AC=EC,
AC=EC,
∴ED=EC=CD,
∴∠ECD=60°,
∴∠A=30°,
∵AC=BC,
∴∠ACB=120°.
(2)∵∠A=30°,AC=BC,
∴∠ABC=30°,
∴∠BCE=60°,
在△ACD与△BCF中

∴△ACD≌△BCF(SAS)
∴∠ADC=∠BFC,
∵CD⊥AB,
∴CF⊥BF,
∵AC=8,CF= AC.
AC.
∴CF=4,
∴AF=12,
∵∠AFB=90°,∠A=30°,
∴BF= AB,
AB,
设BF=x,则AB=2x,
∵AF2+BF2=AB2,
∴(2x)2﹣x2=122
解得:x=4
即BF=4
∴S△ABF=
考点:1、切线的性质;2、等腰三角形的判定与性质;3、勾股定理


科目:初中数学 来源:2014年初中毕业升学考试(江苏镇江卷)数学(解析版) 题型:解答题
读取表格中的信息,解决问题.
n=1 |
|
|
|
n=2 | a2=b1+2c1 | b2=c1+2a1 | c2=a1+2b1 |
n=3 | a3=b2+2c2 | b3=c2+2a2 | c=a2+2b2 |
… | … | … | … |
满足 的n可以取得的最小整数是 .
的n可以取得的最小整数是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏苏州卷)数学(解析版) 题型:解答题
如图,已知⊙O上依次有A,B,C,D四个点, ,连接AB,AD,BD,弦AB不经过圆心O.延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
,连接AB,AD,BD,弦AB不经过圆心O.延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
(1)若⊙O的半径为3,∠DAB=120°,求劣弧 的长;
的长;
(2)求证:BF=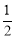 BD;
BD;
(3)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏苏州卷)数学(解析版) 题型:选择题
如图,△AOB为等腰三角形,顶点A的坐标为(2, ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为( )

A.( ,
, ) B.(
) B.( ,
, )
)
C.( ,
, ) D.(
) D.( ,4
,4 )
)
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏淮安卷)数学(解析版) 题型:解答题
如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB、AC于点E、F,连接DE、DF.求证:四边形AEDF是菱形.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:解答题
(1)如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.求证: .(这个比值
.(这个比值
叫做AE与AB的黄金比.)
(2)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.
(注:直尺没有刻度!作图不要求写作法,但要求保留作图痕迹,并对作图中涉及到的点用字母进行标注)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com