Question

如图，已知⊙O上依次有A，B，C，D四个点，，连接AB，AD，BD，弦AB不经过圆心O．延长AB到E，使BE＝AB，连接EC，F是EC的中点，连接BF．

（1）若⊙O的半径为3，∠DAB＝120°，求劣弧的长；

（2）求证：BF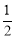＝BD；

（3）设G是BD的中点，探索：在⊙O上是否存在点P（不同于点B），使得PG＝PF?并说明PB与AE的位置关系

 

 

Answer 1

（1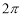）；（2）证明见解析；（3）在⊙O上存在点P（不同于点B），使得PG=PF，此时PB⊥AE.

【解析】

试题分析：（1）要求劣弧BD的长，根据弧长公式，只需求圆心角∠BOD的度数，所以，需要连接OB、OD.由同弧所对的圆周角等于圆心角的一半，可得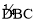所对的圆心角为2400，所以∠BOD=1200.利用弧长公式直接计算可解.

（2）连接AC，则BF是△ACE的中位线，再根据弧弦关系定理，证得AC=BD即可.

（3）作∠DBF的平分线交⊙O于点P，连接PG，PB，则由SAS可证△PBG≌△PGB，从而得到PG-PF，此时，由∠FBE=∠CAE和∠DBA=∠FBE可得∠PBA=∠PBE=900，即 PB⊥AE.

试题解析：【解析】
（1）如答图1， 连接OB、OD，

∵∠DAB=1200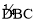，∴所对的圆心角为2400．∴∠BOD=1200．

∵⊙O的半径为3，∴劣弧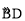的长为.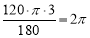

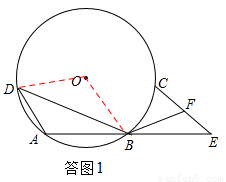
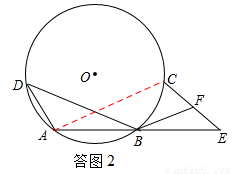
（2）证明：如答图2，连接AC，

∵AB=BE，∴B是AE的中点.

∵F是EC的中点, ∴BF是△EAC的中位线．∴BF=.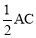

∵，

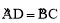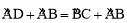∴，即.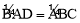

∴BD=AC．∴BF＝.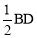

（3）在⊙O上存在点P（不同于点B），使得PG=PF，此时PB⊥AE．理由如下：

如答图3，作∠DBF的平分线交⊙O于点P，连接PG，PB，则

∵G是BD的中点，由（2）BF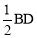＝，∴BG=BF.

又∵PB=PB，∠PBG=∠PBF，

∴△PBG≌△PGB（SAS）．∴PG-PF.

由（2）BF是△EAC的中位线， ∴BF∥AC.

∴∠FBE=∠CAE.

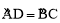∴，∴∠CAB=∠DBA．

∴∠DBA=∠FBE．∴∠PBA=∠PBE=900，即 PB⊥AE.

考点：1.圆周角定理；2．弧长计算；3．三角形的中位线的性质；4．弧弦关系定理；5.全等三角形的判定和性质；6.垂直的判定.