
ij��ѧ��ȤС����߶��ϵĶ����������̽������֪AB=8.
����˼����
��ͼ1����PΪ�߶�AB�ϵ�һ�����㣬�ֱ���AP��BPΪ����ͬ����������APDC��������PBFE.
��1���ڵ�P�˶�ʱ�����������������֮���Ƕ�ֵ�����ʱ����������ǣ�������������������֮�͵���Сֵ.
��2���ֱ�����AD��DF��AF��AF��DP�ڵ�A������P�˶�ʱ������APK����ADK����DFK�У��Ƿ�����������ʼ����ȵ������Σ���˵������.

������չ��
��3����ͼ2����ABΪ����������ABCD������P��Q��������ABCD�ı����˶�����PQ=8.����P�ӵ�A��������A��B��C��D����·����D���˶������P��A��D���˶������У�PQ���е�O��������·���ij���
(4)��ͼ��3�����ڡ�����˼�����У�����M��N���߶�AB�ϵ����㣬��AM=BM=1����G��H�ֱ��DZ�CD��EF���е�.��ֱ��д����P��M��N���˶������У�GH���е�O��������·���ij���OM+OB����Сֵ.


��1����x=4ʱ�����������������֮������Сֵ����СֵΪ32��
��2�������������ʼ����ȵ������Σ�ͼ�μ�������
��3��PQ���е�O��������·���ij�Ϊ6�У�
��4����O��������·����Ϊ3��OM+OB����СֵΪ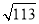 ��
��
��������
�����������1����AP=x����PB=1-x�����������ε������ʽ�õ����������������֮��=x2+��8-x��2���䷽�õ�2��x-4��2+32��Ȼ����ݶ��κ�������ֵ������⣻
��2������PE��BF���PK=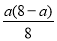 ���������DK=PD-PK=a-
���������DK=PD-PK=a-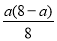 =
=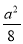 ��Ȼ����������ʽ������ã�
��Ȼ����������ʽ������ã�
��3��PQ���е�O��������·�������ΰ뾶Ϊ4��Բ�Ľ�Ϊ90���Բ����
��4��GH�е�O���˶�·������ABƽ���Ҿ���Ϊ3���߶�XY�ϣ�Ȼ��������ԳƵ����ʣ����OM+OB����Сֵ��
�����������1������P�˶�ʱ�������������ε����֮�Ͳ��Ƕ�ֵ��
��AP=x����PB=8-x��
������������������������֮��=x2+��8-x��2=2x2-16x+64=2��x-4��2+32��
���Ե�x=4ʱ�����������������֮������Сֵ����СֵΪ32��
��2�������������ʼ����ȵ������Σ���������APK����DFK��
�����⻭��ͼ�Σ���ͼ��ʾ��
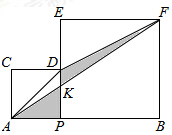
��AP=a����PB=BF=8-a��
��PE��BF��
��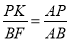 ��
��
��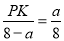 ��
��
��PK=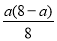 ��
��
��DK=PD-PK= a-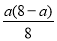 =
=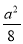 ��
��
��S��APK=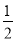 PK•PA=
PK•PA=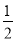 •
•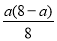 •a=
•a=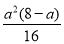 ��S��DFK=
��S��DFK=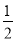 DK•EF=
DK•EF=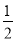 •
•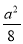 •��8-a��=
•��8-a��=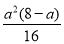 ��
��
��S��APK=S��DFK��
��3������P�ӵ�A��������A��B��C��D����·�����D�˶�ʱ���������Q��DA���ϣ�
����P�ڵ�A����Q�ڵ�D����ʱPQ���е�O��ΪDA�ߵ��е㣻
����Q��DA���ϣ��Ҳ��ڵ�D�����P��AB�ϣ��Ҳ��ڵ�A��
��ʱ��Rt��APQ�У�OΪPQ���е㣬����AO=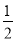 PQ=4��
PQ=4��
���Ե�O����AΪԲ�ģ��뾶Ϊ4��Բ�Ľ�Ϊ90���Բ���ϣ�
PQ���е�O��������·�������ΰ뾶Ϊ4��Բ�Ľ�Ϊ90���Բ������ͼ��ʾ��
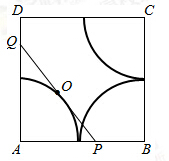
����PQ���е�O��������·���ij�Ϊ��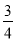 ��2�С�4=6����
��2��4=6����
��4����O��������·����Ϊ3��OM+OB����СֵΪ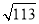 ��
��
��ͼ���ֱ����G��O��H��AB�Ĵ��ߣ�����ֱ�Ϊ��R��S��T�����ı���GRTHΪ���Σ�
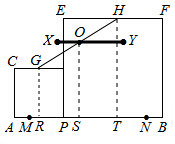
����OΪ�е㣬
��OS=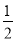 ��GR+HT��=
��GR+HT��=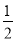 ��AP+PB��=4����OSΪ��ֵ��
��AP+PB��=4����OSΪ��ֵ��
����O���˶�·������AB����Ϊ4��ƽ�����ϣ�
��MN=6����P���߶�MN���˶����ҵ�OΪGH�е㣬
����O���˶�·��Ϊ�߶�XY��XY=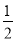 MN=3��XY��AB��ƽ����֮�����Ϊ4����X���A����Y���B֮���ˮƽ�����Ϊ2.5��
MN=3��XY��AB��ƽ����֮�����Ϊ4����X���A����Y���B֮���ˮƽ�����Ϊ2.5��
��ͼ������M����ֱ��XY�ĶԳƵ�M�䣬����BM�䣬��XY���ڵ�O��
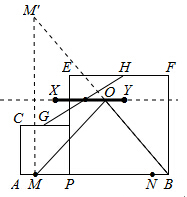
����Գ����ʿ�֪����ʱOM+OB=BM����С��
��Rt��BMM���У��ɹ��ɶ����ã�BM��=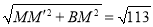 ��
��
��OM+OB����СֵΪ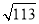 ��
��
���㣺�ı����ۺ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭����������ѧ�������棩 ���ͣ������
ij������һ���۳����ֿ�ζѩ������������ͳ��ͼ��ͼ��ʾ�������۳��춹��ζ��ѩ��200֧����ô�۳�ˮ����ζѩ��������� ֧

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�����������ѧ�������棩 ���ͣ������
��ͼ1����ƽ��ֱ������ϵxOy�У���MΪ������ �Ķ��㣬���㣨0��4����x���ƽ���ߣ����������ڵ�P��Q����P��Q����ࣩ��PQ=4��
�Ķ��㣬���㣨0��4����x���ƽ���ߣ����������ڵ�P��Q����P��Q����ࣩ��PQ=4��
��1���������ߵĺ�����ϵʽ����д����P�����ꣻ
��2��С�����֣��������� ���ŵ�P��ת180�㣬�����������ߵĶ���ǡΪ����ԭ��O������Ϊ��ȷ����˵�����ɣ�
���ŵ�P��ת180�㣬�����������ߵĶ���ǡΪ����ԭ��O������Ϊ��ȷ����˵�����ɣ�
��3����ͼ2����֪��A��1��0������PAΪ��������PABC����P��A��B��C��˳ʱ��ķ������У��� ��
��
��д��C������꣺C�� �� ���������ú���t�Ĵ���ʽ��ʾ����
������C���⣨2������ת������������ϣ���t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�����������ѧ�������棩 ���ͣ������
��ȡ�����е���Ϣ���������.
n=1 |
|
|
|
n=2 | a2=b1+2c1 | b2=c1+2a1 | c2=a1+2b1 |
n=3 | a3=b2+2c2 | b3=c2+2a2 | c=a2+2b2 |
�� | �� | �� | �� |
���� ��n����ȡ�õ���С������ ��
��n����ȡ�õ���С������ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�����������ѧ�������棩 ���ͣ������
��ͼ��CD����ABC�����ߣ���E��F�ֱ���AC��DC���е㣬EF=1��BD= ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������Ƹ۾�����ѧ�������棩 ���ͣ������
��ͼ1����һ�������Ĵ�����װ���ĸ��ֱ������ĸA��B��C��D����Щ�������ĸ����ȫ��ͬ�����⣬��һ���ɫ����һ���ɫ����С��ͬ�����������ο�Ƭ��ÿ�ſ�Ƭ�������ĸ��ͬ���ֱ������ĸA��B��C��D��������ڳ���ͼ2�����ӣ�A��D�Ǻ�ɫ��B��C�ǰ�ɫ.


���β�����۲쿨Ƭ����ɫ��
���磺��һ��ȡ��A���ڶ���ȡ��B����ʱ��Ƭ����ɫ��� ��
��
��1��ȡ���ſ�Ƭ�����ͬ��ɫ�ĸ��ʣ�
��2�������ſ�Ƭ����������ס���ǡ���γɸ�����ɫ�ľ��εĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������Ƹ۾�����ѧ�������棩 ���ͣ������
��ͼ1�����߶�AOB�����ΪS����O�ֳ��������Σ������Ρ�С���ε�����ֱ�Ϊ ��
�� ����
���� =0.618����Ʒֳɵ�С����Ϊ���ƽ����Ρ��������е����ȣ���ͼ2���������ǡ��ƽ����Ρ����ƽ����Ρ���Բ�Ľ�ԼΪ ��.(��ȷ��0.1)
=0.618����Ʒֳɵ�С����Ϊ���ƽ����Ρ��������е����ȣ���ͼ2���������ǡ��ƽ����Ρ����ƽ����Ρ���Բ�Ľ�ԼΪ ��.(��ȷ��0.1)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������ݾ�����ѧ�������棩 ���ͣ������
��ͼ����֪��O��������A��B��C��D�ĸ��㣬 ������AB��AD��BD����AB������Բ��O���ӳ�AB��E��ʹBE��AB������EC��F��EC���е㣬����BF��
������AB��AD��BD����AB������Բ��O���ӳ�AB��E��ʹBE��AB������EC��F��EC���е㣬����BF��
��1������O�İ뾶Ϊ3����DAB��120�㣬���ӻ� �ij���
�ij���
��2����֤��BF��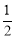 BD��
BD��
��3����G��BD���е㣬̽��������O���Ƿ���ڵ�P����ͬ�ڵ�B����ʹ��PG��PF?��˵��PB��AE��λ�ù�ϵ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ����ջ���������ѧ�������棩 ���ͣ������
��m2��2m��1=0�������ʽ2m2��4m+3��ֵΪ�� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com