
ШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуMЮЊХзЮяЯп ЕФЖЅЕуЃЌЙ§ЕуЃЈ0ЃЌ4ЃЉзїxжсЕФЦНааЯпЃЌНЛХзЮяЯпгкЕуPЁЂQЃЈЕуPдкQЕФзѓВрЃЉЃЌPQ=4ЃЎ
ЕФЖЅЕуЃЌЙ§ЕуЃЈ0ЃЌ4ЃЉзїxжсЕФЦНааЯпЃЌНЛХзЮяЯпгкЕуPЁЂQЃЈЕуPдкQЕФзѓВрЃЉЃЌPQ=4ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЕуPЕФзјБъЃЛ
ЃЈ2ЃЉаЁРіЗЂЯжЃКНЋХзЮяЯп ШЦзХЕуPа§зЊ180ЁуЃЌЫљЕУаТХзЮяЯпЕФЖЅЕуЧЁЮЊзјБъдЕуOЃЌФуШЯЮЊе§ШЗТ№ЃПЧыЫЕУїРэгЩЃЛ
ШЦзХЕуPа§зЊ180ЁуЃЌЫљЕУаТХзЮяЯпЕФЖЅЕуЧЁЮЊзјБъдЕуOЃЌФуШЯЮЊе§ШЗТ№ЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌвбжЊЕуAЃЈ1ЃЌ0ЃЉЃЌвдPAЮЊБпзїОиаЮPABCЃЈЕуPЁЂAЁЂBЁЂCАДЫГЪБеыЕФЗНЯђХХСаЃЉЃЌ ЃЎ
ЃЎ
ЂйаДГіCЕуЕФзјБъЃКCЃЈ ЃЌ ЃЉЃЈзјБъгУКЌгаtЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЂкШєЕуCдкЬтЃЈ2ЃЉжаа§зЊКѓЕФаТХзЮяЯпЩЯЃЌЧѓtЕФжЕЃЎ

ЃЈ1ЃЉ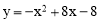 ЃЛЃЈ2ЃЌ4ЃЉЃЛЃЈ2ЃЉе§ШЗЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉЂй-4t+2ЃЌ4+tЃЛЂк
ЃЛЃЈ2ЃЌ4ЃЉЃЛЃЈ2ЃЉе§ШЗЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉЂй-4t+2ЃЌ4+tЃЛЂк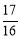 .
.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉАбPЕФзнзјБъДњШыХзЮяЯпЕФНтЮіЪНЕУЕНЙигкxЕФЗНГЬЃЌИљОнИљгыЯЕЪ§ЕФЙиЯЕЧѓЕУКЭPQ=4ЃЌЧѓЕУnЕФжЕЃЌМДПЩЧѓЕУНтЮіЪН.
ЃЈ2ЃЉИљОна§зЊЕФаджЪЕУЕНQШЦзХЕуPа§зЊ180ЁуКѓЕФЖдГЦЕуЮЊQЁфЃЈ-2ЃЌ4ЃЉЃЌЕУГіаТХзЮяЯпЕФЖдГЦжсЪЧyжсЃЌШЛКѓЧѓЕУХзЮяЯпЕФЖЅЕуЕНжБЯпPQЕФОрРыЮЊ4ЃЌМДПЩХаЖЯаТХзЮяЯпЖЅЕугІЮЊзјБъдЕуЃЎ
ЃЈ3ЃЉЂйИљОнШ§НЧаЮЯрЫЦМДПЩЧѓЕУCЕФзјБъЃК
ШчД№ЭМЃЌЙ§PзїxжсЕФДЙЯпЃЌНЛxжсгкMЃЌЙ§CзїCNЁЭMNгкNЃЌ
Ёп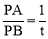 ЃЌЁр
ЃЌЁр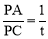 .
.
ЁпвзЕУЁїAPMЁзЁїPCNЃЌЁр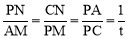 .
.
ЁпAM=2-1=1ЃЌPM=4ЃЌЁрPN=tЃЌCN=4t.
ЁрMN=4+t.
ЁрCЃЈ-4t+2ЃЌ4+tЃЉЃЌ
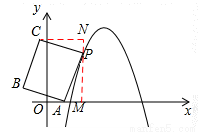
ЂкгЩЃЈ1ЃЉПЩжЊЃЌа§зЊКѓЕФаТХзЮяЯпЪЧ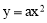 ЃЌаТХзЮяЯпЪЧ
ЃЌаТХзЮяЯпЪЧ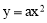 Й§PЃЈ2ЃЌ4ЃЉЃЌЧѓЕУаТХзЮяЯпЕФНтЮіЪНЃЌАбCЃЈ-4t+2ЃЌ4+tЃЉДњШыМДПЩЧѓЕУtЕФжЕЃЎ
Й§PЃЈ2ЃЌ4ЃЉЃЌЧѓЕУаТХзЮяЯпЕФНтЮіЪНЃЌАбCЃЈ-4t+2ЃЌ4+tЃЉДњШыМДПЩЧѓЕУtЕФжЕЃЎ
ЪдЬтНтЮіЃКЁОНтЮіЁП
ЃЈ1ЃЉЁпХзЮяЯп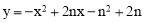 Й§ЕуPЃЌPЕуЕФзнзјБъЮЊ4ЃЌ
Й§ЕуPЃЌPЕуЕФзнзјБъЮЊ4ЃЌ
Ёр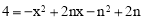 МД
МД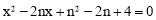 .
.
Ёр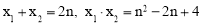 .
.
ЁпPQ=4ЃЌЁр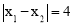 ЃЌМД
ЃЌМД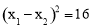 ЃЌМД
ЃЌМД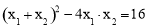 .
.
Ёр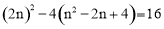 ЃЌНтЕУЃКn=4.
ЃЌНтЕУЃКn=4.
ЁрХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЮЊЃК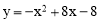 .
.
гЩ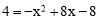 НтЕУx=2Лђx=6.
НтЕУx=2Лђx=6.
ЁрPЃЈ2ЃЌ4ЃЉЃЎ
ЃЈ2ЃЉе§ШЗЃЌРэгЩШчЯТЃК
ЁпPЃЈ2ЃЌ4ЃЉЃЌPQ=4ЃЌЁрQШЦзХЕуPа§зЊ180ЁуКѓЕФЖдГЦЕуЮЊQЁфЃЈ-2ЃЌ4ЃЉ.
ЁрPгыQЁфе§КУЙигкyжсЖдГЦ.
ЁрЫљЕУаТХзЮяЯпЕФЖдГЦжсЪЧyжсЃЌ
ЁпХзЮяЯп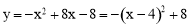 ЃЌЁрХзЮяЯпЕФЖЅЕуMЃЈ4ЃЌ8ЃЉ.
ЃЌЁрХзЮяЯпЕФЖЅЕуMЃЈ4ЃЌ8ЃЉ.
ЁрЖЅЕуMЕНжБЯпPQЕФОрРыЮЊ4.
ЁрЫљЕУаТХзЮяЯпЖЅЕуЕНжБЯпPQЕФОрРыЮЊ4.
ЁрЫљЕУаТХзЮяЯпЖЅЕугІЮЊзјБъдЕуЃЎ
ЃЈ3ЃЉЂй-4t+2ЃЌ4+t.
ЂкгЩЃЈ1ЃЉПЩжЊЃЌа§зЊКѓЕФаТХзЮяЯпЪЧ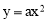 ЃЌ
ЃЌ
ЁпаТХзЮяЯп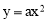 Й§PЃЈ2ЃЌ4ЃЉЃЌЁр4=4aЃЌНтЕУa=1.
Й§PЃЈ2ЃЌ4ЃЉЃЌЁр4=4aЃЌНтЕУa=1.
Ёра§зЊКѓЕФаТХзЮяЯпЪЧ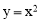 .
.
ЁпCЃЈ-4t+2ЃЌ4+tЃЉдкХзЮяЯп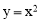 ЩЯЃЌ
ЩЯЃЌ
Ёр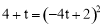 ЃЌНтЕУЃКt=0ЃЈЩсШЅЃЉЛђt=
ЃЌНтЕУЃКt=0ЃЈЩсШЅЃЉЛђt=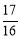 .
.
Ёрt=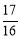 .
.
ПМЕуЃК1.ЖўДЮКЏЪ§злКЯЬтЃЛ2.ЯпЖЏа§зЊЮЪЬтЃЛ3.ЧњЯпЩЯЕуЕФзјБъгыЗНГЬЕФЙиЯЕЃЛ4.вЛдЊЖўДЮЗНГЬИљгыЯЕЪ§ЕФЙиЯЕЃЛ5.ЖўДЮКЏЪ§ЕФаджЪЃЛ6. а§зЊКЭжсЖдГЦЕФаджЪЃЛ7.ЗНГЬЫМЯыЕФгІгУ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈеуНКМжнОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
дкЁїABCжаЃЌAB=ACЃЌЕуE,FЗжБ№дкAB,ACЩЯЃЌAE=AFЃЌBFгыCEЯрНЛгкЕуPЃЌЧѓжЄЃКPB=PCЃЌВЂЧыжБНгаДГіЭМжаЦфЫћЯрЕШЕФЯпЖЮ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈеуНФўВЈОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
гУОиаЮжНЦЌелГіжБНЧЕФЦНЗжЯпЃЌЯТСаелЗЈе§ШЗЕФЪЧ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈНЮїФЯВ§ОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ШчЭМ1ЃЌНЋвЛИіБпГЄЮЊaЕФе§ЗНаЮжНЦЌМєШЅСНИіаЁОиаЮЃЌЕУЕНвЛИіЁА ЁБЕФЭМАИЃЌШчЭМ2ЫљЪОЃЌдйНЋМєЯТЕФСНИіаЁОиаЮЦДГЩвЛИіаТЕФОиаЮЃЌШчЭМ3ЫљЪОЃЌдђаТОиаЮЕФжмГЄПЩБэЪОЮЊЃЈЁЁЁЁЃЉ
ЁБЕФЭМАИЃЌШчЭМ2ЫљЪОЃЌдйНЋМєЯТЕФСНИіаЁОиаЮЦДГЩвЛИіаТЕФОиаЮЃЌШчЭМ3ЫљЪОЃЌдђаТОиаЮЕФжмГЄПЩБэЪОЮЊЃЈЁЁЁЁЃЉ

AЃЎ2aЉ3b BЃЎ4aЉ8b CЃЎ2aЉ4b DЃЎ4aЉ10b
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈНЮїФЯВ§ОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ЯТСадЫЫуе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
AЃЎa2+a3=a5 BЃЎЃЈЉ2a2ЃЉ3=Љ6a6 CЃЎЃЈ2a+1ЃЉЃЈ2aЉ1ЃЉ=2a2Љ1 DЃЎЃЈ2a3Љa2ЃЉЁТa2=2aЉ1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈНЫееђНОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
дквЛжЛВЛЭИУїЕФВМДќжазАгаКьЧђЁЂЛЦЧђИїШєИЩИіЃЌетаЉЧђГ§беЩЋЭтЖМЯрЭЌЃЌОљдШвЁдШ.
ЃЈ1ЃЉШєВМДќжага3ИіКьЧђЃЌ1ИіЛЦЧђЃЎДгВМДќжавЛДЮУўГі2ИіЧђЃЌМЦЫуЁАУўГіЕФЧђЧЁЪЧвЛКьвЛЛЦЁБЕФИХТЪЃЈгУЁАЛЪїзДЭМЁБЛђЁАСаБэЁБЕФЗНЗЈаДГіМЦЫуЙ§ГЬЃЉЃЛ
ЃЈ2ЃЉШєВМДќжага3ИіКьЧђЃЌxИіЛЦЧђЃЎ
ЧыаДГівЛИіxЕФжЕ ЃЌЪЙЕУЪТМўЁАДгВМДќжавЛДЮУўГі4ИіЧђЃЌЖМЪЧЛЦЧђЁБЪЧВЛПЩФмЕФЪТМўЃЛ
ЃЈ3ЃЉШєВМДќжага3ИіКьЧђЃЌ4ИіЛЦЧђЃЎ
ЮвУЧжЊЕРЃКЁАДгДќжавЛДЮУўГі4ИіЧђЃЌжСЩйгавЛИіЛЦЧђЁБЮЊБиШЛЪТМўЃЎ
ЧыФуЗТееетИіБэЪіЃЌЩшМЦвЛИіБиШЛЪТМўЃК ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈНЫееђНОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
вбжЊЙ§Еу ЕФжБЯп
ЕФжБЯп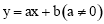 ВЛОЙ§ЕквЛЯѓЯо.Щш
ВЛОЙ§ЕквЛЯѓЯо.Щш ЃЌдђsЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЃЌдђsЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A. B.
B.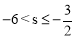 C.
C. D.
D.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈНЫеСЌдЦИлОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
ФГЪ§бЇаЫШЄаЁзщЖдЯпЖЮЩЯЕФЖЏЕуЮЪЬтНјааЬНОПЃЌвбжЊAB=8.
ЮЪЬтЫМПМЃК
ШчЭМ1ЃЌЕуPЮЊЯпЖЮABЩЯЕФвЛИіЖЏЕуЃЌЗжБ№вдAPЁЂBPЮЊБпдкЭЌВрзїе§ЗНаЮAPDCгые§ЗНаЮPBFE.
ЃЈ1ЃЉдкЕуPдЫЖЏЪБЃЌетСНИіе§ЗНаЮУцЛ§жЎКЭЪЧЖЈжЕТ№ЃПШчЙћЪБЧѓГіЃЛШєВЛЪЧЃЌЧѓГіетСНИіе§ЗНаЮУцЛ§жЎКЭЕФзюаЁжЕ.
ЃЈ2ЃЉЗжБ№СЌНгADЁЂDFЁЂAFЃЌAFНЛDPгкЕуAЃЌЕБЕуPдЫЖЏЪБЃЌдкЁїAPKЁЂЁїADKЁЂЁїDFKжаЃЌЪЧЗёДцдкСНИіУцЛ§ЪМжеЯрЕШЕФШ§НЧаЮЃПЧыЫЕУїРэгЩ.

ЮЪЬтЭиеЙЃК
ЃЈ3ЃЉШчЭМ2ЃЌвдABЮЊБпзїе§ЗНаЮABCDЃЌЖЏЕуPЁЂQдке§ЗНаЮABCDЕФБпЩЯдЫЖЏЃЌЧвPQ=8.ШєЕуPДгЕуAГіЗЂЃЌбиAЁњBЁњCЁњDЕФЯпТЗЃЌЯђDЕудЫЖЏЃЌЧѓЕуPДгAЕНDЕФдЫЖЏЙ§ГЬжаЃЌPQЕФжаЕуOЫљОЙ§ЕФТЗОЖЕФГЄЁЃ
(4)ШчЭМЃЈ3ЃЉЃЌдкЁАЮЪЬтЫМПМЁБжаЃЌШєЕуMЁЂNЪЧЯпЖЮABЩЯЕФСНЕуЃЌЧвAM=BM=1ЃЌЕуGЁЂHЗжБ№ЪЧБпCDЁЂEFЕФжаЕу.ЧыжБНгаДГіЕуPДгMЕНNЕФдЫЖЏЙ§ГЬжаЃЌGHЕФжаЕуOЫљОЙ§ЕФТЗОЖЕФГЄМАOM+OBЕФзюаЁжЕ.


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈНЫеЫежнОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
ШчЭМЃЌдкЁїABCжаЃЌABЃНACЃН5ЃЌBCЃН8ЃЎШєЁЯBPCЃН ЁЯBACЃЌдђtanЁЯBPCЃН ЃЎ
ЁЯBACЃЌдђtanЁЯBPCЃН ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com