
如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.
(1)求证:AC∥DE;
(2)求证:过点B作BF⊥AC与点F,连接EF,试判断四边形BCEF的形状,并说明理由.

证明:(1)在矩形ABCD中,AB∥CD ∴∠CAB=∠DCA
∵∠EDC=∠CAB ∴∠EDC=∠DCA
∴AC∥DE ……………………………………………………………………………4分
(2)四边形BCEF为平行四边形
∵BF⊥AC ∴∠AFB=90°
∵∠E DC=∠CAB ∠DEC=∠AFB=90° CD=AB …………………………6分
DC=∠CAB ∠DEC=∠AFB=90° CD=AB …………………………6分
∴△DEC ≌△AFB
∴EC=FB ∠ECD=∠FBA ………………………………………………………6分
∵∠FBA+∠FBC=90° ∴∠ECD +∠DCB+∠FBC=180° ∴EC∥FB ………8分
∴四边形BCEF为平行四边形 ……………………………………………………10分


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
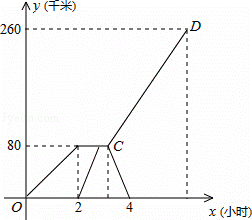
已知,A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,结合图象回答下列问题:
(1)甲车提速后的速度是 千米/时,乙车的速度是 千米/时,点C的坐标为 ;
(2)求乙车返回时y与x的函数关系式并写出自变量x的取值范围;
(3)求甲车到达B市时乙车已返回A市多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
为了了解某校八年级40 0名学生的体重情况,从中抽查了50名学生的体重进行统计分析,在这个问题中,总体是指 ( )
0名学生的体重情况,从中抽查了50名学生的体重进行统计分析,在这个问题中,总体是指 ( )
A 400名学生 B 被抽取的50名学生 C 400名 学生的体重 D 被抽取的50名学生的体重
学生的体重 D 被抽取的50名学生的体重
查看答案和解析>>
科目:初中数学 来源: 题型:
下列计算正确的是………………………………………………………………( )
A.x3+ x3=x6 B.x3÷x4=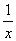 C.(m5)5=m10 D.x2y3=(xy)5
C.(m5)5=m10 D.x2y3=(xy)5
查看答案和解析>>
科目:初中数学 来源: 题型:
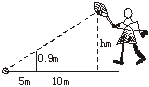
已知如图,小明在打网球时,要使球恰好能打过网,而且落在离网5 m的 位置上,则球拍击球的高度h应为( )
位置上,则球拍击球的高度h应为( )
A、2.7 m B、1.8 m C、0.9 m D、6 m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com