
【题目】如图,在矩形![]() 中,点
中,点![]() 为对角线
为对角线![]() 的中点,点
的中点,点![]() 是
是![]() 上一点,连接
上一点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
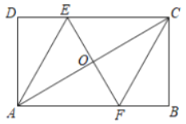
(1)求证:![]() ;
;
(2)当![]() 时,试判断四边形
时,试判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)证明见解析;(2)四边形![]() 是菱形,理由见解析.
是菱形,理由见解析.
【解析】
(1)先根据矩形的性质得出![]() ,再根据平行线的性质可得
,再根据平行线的性质可得![]() ,然后根据线段中点的定义可得
,然后根据线段中点的定义可得![]() ,最后根据三角形全等的判定定理即可得证;
,最后根据三角形全等的判定定理即可得证;
(2)先根据三角形全等的性质得出![]() ,再根据平行四边形的判定可得四边形
,再根据平行四边形的判定可得四边形![]() 是平行四边形,然后根据平行线的性质、角的和差可得
是平行四边形,然后根据平行线的性质、角的和差可得![]() ,又根据等腰三角形的三线合一可得
,又根据等腰三角形的三线合一可得![]() ,从而根据菱形的判定可得平行四边形
,从而根据菱形的判定可得平行四边形![]() 是菱形,最后说明菱形
是菱形,最后说明菱形![]() 不是正方形即可.
不是正方形即可.
(1)![]() 四边形ABCD是矩形
四边形ABCD是矩形
![]() ,
,![]()
![]()
![]() 点O是对角线
点O是对角线![]() 的中点
的中点
![]()
在![]() 和
和![]() 中,
中,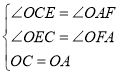
![]() ;
;
(2)四边形![]() 是菱形,理由如下:
是菱形,理由如下:
由(1)已证:![]()
![]()
又![]() ,即
,即![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]()
![]()
![]() ,即OA是
,即OA是![]() 的角平分线
的角平分线
![]() (等腰三角形的三线合一)
(等腰三角形的三线合一)
![]() 平行四边形
平行四边形![]() 是菱形
是菱形
![]() 点
点![]() 是
是![]() 上一点,
上一点,![]()
![]() ,即
,即![]()
![]() 菱形
菱形![]() 不是正方形
不是正方形
综上,四边形![]() 是菱形.
是菱形.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y = x2 – 2 m x – 2m – 2与直线y =-x-2 交于C,D两点,将抛物线在C、D两点之间的部分(不含C、D)上恰有两个点的横坐标为整数,则m的取值范围为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2![]() ,∠ABC=60°,点E、F在对角线BD上运动,且EF=2,连接AE、AF,则△AEF周长的最小值是( )
,∠ABC=60°,点E、F在对角线BD上运动,且EF=2,连接AE、AF,则△AEF周长的最小值是( )
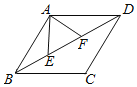
A.4B.4+![]() C.2+2
C.2+2![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C.
(1)求a,b的值
(2)若点D是抛物线上的一点,且位于直线BC上方,连接CD,BD,AC.当四边形ABDC的面积有最大值时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该芒果在一天内的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)之间的数量满足如下表所示的一次函数关系.
(元/千克)之间的数量满足如下表所示的一次函数关系.
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
(1)某天这种芒果售价为28元/千克.求当天该芒果的销售量
(2)设某天销售这种芒果获利![]() 元,写出
元,写出![]() 与售价
与售价![]() 之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校为了了解图书漂流的开展情况,随机抽取部分学生进行了问卷调查,选项![]() :阅读漂流图书
:阅读漂流图书![]() 本及以上;选项
本及以上;选项![]() :阅读漂流图书
:阅读漂流图书![]() 本;选项
本;选项![]() :阅读漂流图书
:阅读漂流图书![]() 本;选项
本;选项![]() :没有阅读漂流图书,只能从中选择一个选项进行回答.收集整理问卷调查的情况,把结果绘制成如下不完整的统计图:
:没有阅读漂流图书,只能从中选择一个选项进行回答.收集整理问卷调查的情况,把结果绘制成如下不完整的统计图:
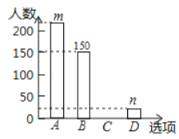
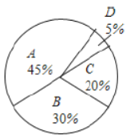
(1)此次抽样调查了_______名学生;
(2)补全条形统计图;
(3)扇形统计图![]() 选项圆心角的度数是_______;
选项圆心角的度数是_______;
(4)该校有![]() 名学生,估计全校阅读过漂流图书的学生约有多少名?
名学生,估计全校阅读过漂流图书的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
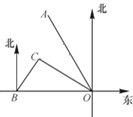
【题目】如图所示,港口B位于港口O正西方向120 km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以v km/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60 km/h的速度驶向小岛C,在小岛C用1 h加装补给物资后,立即按原来的速度给游船送去.
(1)快艇从港口B到小岛C需要多长时间?
(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com