
【题目】如图,抛物线y=ax2+bx+2与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C.
(1)求a,b的值
(2)若点D是抛物线上的一点,且位于直线BC上方,连接CD,BD,AC.当四边形ABDC的面积有最大值时,求点D的坐标.

【答案】(1)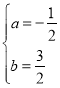 ;(2)点D的坐标为(2,3).
;(2)点D的坐标为(2,3).
【解析】
(1)用待定系数法解答便可;
(2)先用待定系数法求出BC的解析式,过点D作直线DE∥y轴,交BC于点E,设D点的横坐标为n,用n表示DE,再由三角形的面积公式,列出面积关于n的二次函数解析式,再根据二次函数的最值的求法求n便可.
解:(1)把A(﹣1,0),B(4,0)代入y=ax2+bx+2中,得
![]() .
.
∴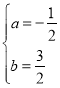 ;
;
(2)设直线BC的表达式为y=kx+h,
将B(4,0),C(0,2)分别代入,
得![]()
解得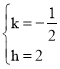
故直线BC的表达式为![]() .
.
过点D作直线DE∥y轴,交BC于点E,

∵抛物线y=ax2+bx+2=2=﹣![]() ,
,
∴设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() +4n=﹣(n﹣2)2+4,
+4n=﹣(n﹣2)2+4,
根据二次函数的性质可知,当n=2时,S△BCD取最大值,
此时点D的坐标为(2,3).


科目:初中数学 来源: 题型:
【题目】如图1,经过点B(1,0)的抛物线![]() 与y轴交于点C,其顶点为点G,过点C作y轴的垂线交抛物线对称轴于点D,线段CO上有一动点M,连接DM、DG.
与y轴交于点C,其顶点为点G,过点C作y轴的垂线交抛物线对称轴于点D,线段CO上有一动点M,连接DM、DG.
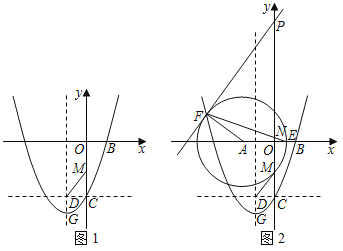
(1)求抛物线的表达式;
(2)求![]() 的最小值以及相应的点M的坐标;
的最小值以及相应的点M的坐标;
(3)如图2,在(2)的条件下,以点A(﹣2,0)为圆心,以AM长为半径作圆交x轴正半轴于点E.在y轴正半轴上有一动点P,直线PF与⊙A相切于点F,连接EF交y轴于点N,当PF∥BM时,求PN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料69千克,乙种原料52千克,现计划用这两种原料生产A,B两种型号的产品共80件,已知每件A型号产品需要甲种原料0.6千克,乙种原料0.9千克;每件B型号产品需要甲种原料1.1千克,乙种原料0.4千克.请解答下列问题:
(1)该工厂有哪几种生产方案?
(2)在这批产品全部售出的条件下,若1件A型号产品获利35元,1件B型号产品获利25元,(1)中哪种方案获利最大?最大利润是多少?
(3)在(2)的条件下,工厂决定将所有利润的25%全部用于再次购进甲、乙两种原料,要求每种原料至少购进4千克,且购进每种原料的数量均为整数.若甲种原料每千克40元,乙种原料每千克60元,请直接写出购买甲、乙两种原料之和最多的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寿春路桥(如图①)横跨合肥市母亲河﹣南淝河,它位于合肥市东西交通主干道寿春路上,建成于1987年年底,为中承式钢筋砼(tong)拱桥,桥的上部结构为2个钢筋混凝土半月形拱肋,如图②是桥拱肋的简化示意图,其中拱宽(弦AB)约100米.
(1)在图②中,请你用尺规作图的方法首先找出弧AB所在圆的圆心O,然后确定弧AB、弦AB的中点C、D.(不要写作法,但保留作图痕迹)
(2)在图②中,若∠AOB=80°,求该拱桥高CD约为多少米?(结果精确到0.1米,参考数据:sin50°≈0.77,cos50°≈0.6,tan50°≈1.19)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=1,BC=3,AC和BD交于点O,点E是边BC上的动点(不与点B,C重合),连接EO并延长交AD于点F,连接AE,若△AEF是等腰三角形,则DF的长为_____.
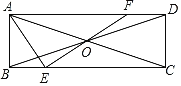
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:
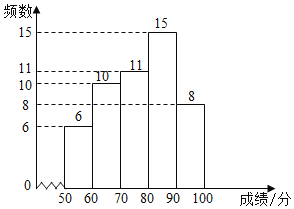
b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后回答问题:
已知a>0,S1=![]() ,S2=﹣S1﹣1,S3=
,S2=﹣S1﹣1,S3=![]() ,S4=﹣S3﹣1,S5=
,S4=﹣S3﹣1,S5=![]() ,….当n为大于1的奇数时,Sn=
,….当n为大于1的奇数时,Sn=![]() ;当n为大于1的偶数时,Sn=﹣Sn﹣1﹣1.直接写出S2020=_____(用含a的代数式表示);计算:S1+S2+S3+…+S2022=_____.
;当n为大于1的偶数时,Sn=﹣Sn﹣1﹣1.直接写出S2020=_____(用含a的代数式表示);计算:S1+S2+S3+…+S2022=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.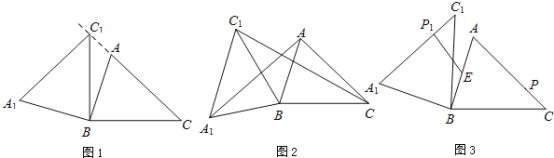
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com