
【题目】某工厂有甲种原料69千克,乙种原料52千克,现计划用这两种原料生产A,B两种型号的产品共80件,已知每件A型号产品需要甲种原料0.6千克,乙种原料0.9千克;每件B型号产品需要甲种原料1.1千克,乙种原料0.4千克.请解答下列问题:
(1)该工厂有哪几种生产方案?
(2)在这批产品全部售出的条件下,若1件A型号产品获利35元,1件B型号产品获利25元,(1)中哪种方案获利最大?最大利润是多少?
(3)在(2)的条件下,工厂决定将所有利润的25%全部用于再次购进甲、乙两种原料,要求每种原料至少购进4千克,且购进每种原料的数量均为整数.若甲种原料每千克40元,乙种原料每千克60元,请直接写出购买甲、乙两种原料之和最多的方案.
【答案】(1)有3种购买方案:方案1,生产A型号产品38件,生产B型号产品42件;方案2,生产A型号产品39件,生产B型号产品41件;方案3,生产A型号产品40件,生产B型号产品40件.(2)生产A型号产品40件,B型号产品40件时获利最大,最大利润为2400元.(3)购买甲种原料9千克,乙种原料4千克.
【解析】
(1)设生产A型号产品x件,则生产B型号产品(80﹣x)件,根据原材料的数量与每件产品的用量建立不等式组,求出其解即可;
(2)设所获利润为W元,根据总利润=A型号产品的利润+B型号产品的利润建立W与x之间的函数关系式,求出其解即可;
(3)根据(2)的结论,设购买甲种原料m千克,购买乙种原料n千克,建立方程,根据题意只有n最小,m最大才可以得出m+n最大得出结论.
解:(1)设生产A型号产品x件,则生产B型号产品(80﹣x)件,由题意,得
![]() ,
,
解得:38≤x≤40.
∵x为整数,
∴x=38,39,40,
∴有3种购买方案:
方案1,生产A型号产品38件,生产B型号产品42件;
方案2,生产A型号产品39件,生产B型号产品41件;
方案3,生产A型号产品40件,生产B型号产品40件.
(2)设所获利润为W元,由题意,得
W=35x+25(80﹣x),
w=10x+2000,
∴k=10>0,
∴W随x的增大而增大,
∴当x=40时.W最大=2400元.
∴生产A型号产品40件,B型号产品40件时获利最大,最大利润为2400元.
(3)设购买甲种原料m千克,购买乙种原料n千克,由题意,得
40m+60n=2400×25%,
即2m+3n=30.
∵m+n要最大,
∴n要最小.
∵m≥4,n≥4,
∴n=4.
∴m=9.
∴购买甲种原料9千克,乙种原料4千克.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】每年的3月15日是“国际消费者权益日”,许多家居商城都会利用这个契机进行打折促销活动.甲卖家的某款沙发每套成本为5000元,在标价8000元的基础上打9折销售.
(1)现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于20%?
(2)据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售相同的沙发,其成本、标价与甲卖家一致,以前每周可售出8套,现乙卖家先将标价提高![]() ,再大幅降价
,再大幅降价![]() 元,使得这款沙发在3月15日那一天卖出的数量就比原来一周卖出的数量增加了
元,使得这款沙发在3月15日那一天卖出的数量就比原来一周卖出的数量增加了![]() ,这样一天的利润达到了50000元,求
,这样一天的利润达到了50000元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y = x2 – 2 m x – 2m – 2与直线y =-x-2 交于C,D两点,将抛物线在C、D两点之间的部分(不含C、D)上恰有两个点的横坐标为整数,则m的取值范围为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E.将△BDE沿直线DE折叠,得到△B′DE,若B′D,B′E分别交AC于点F,G,连接OF,OG,则下列判断错误的是( )
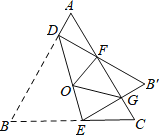
A. △ADF≌△CGE
B. △B′FG的周长是一个定值
C. 四边形FOEC的面积是一个定值
D. 四边形OGB'F的面积是一个定值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2![]() ,∠ABC=60°,点E、F在对角线BD上运动,且EF=2,连接AE、AF,则△AEF周长的最小值是( )
,∠ABC=60°,点E、F在对角线BD上运动,且EF=2,连接AE、AF,则△AEF周长的最小值是( )
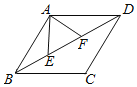
A.4B.4+![]() C.2+2
C.2+2![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C.
(1)求a,b的值
(2)若点D是抛物线上的一点,且位于直线BC上方,连接CD,BD,AC.当四边形ABDC的面积有最大值时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com