
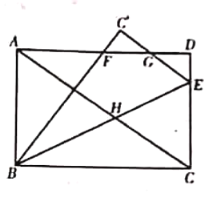
【题目】如图,在矩形![]() 中,点
中,点![]() 在
在![]() 上,连接
上,连接![]() ,将
,将![]() 沿
沿![]() 折叠得到
折叠得到![]() 分别交
分别交![]() 于点
于点![]() .已知
.已知![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 的长为________
的长为________
【答案】![]()
【解析】
延长BE、AD相交于M,由![]() 可得DM=2DE;设DE=a(a>0),则GE=
可得DM=2DE;设DE=a(a>0),则GE=![]() ,
,![]() =7+
=7+![]() ;根据折叠的性质可得CE=
;根据折叠的性质可得CE=![]() =7+
=7+![]() ,BC=
,BC=![]() ,∠D=∠D`;根据矩形的性质可得AM∥BC,AB∥CD,AB=CD, ∠D=∠D`=90°,则∠MBC=∠M;再判定△DGE≌△C`GF,即FC’=DE=a,FG=GE;由tan∠M=
,∠D=∠D`;根据矩形的性质可得AM∥BC,AB∥CD,AB=CD, ∠D=∠D`=90°,则∠MBC=∠M;再判定△DGE≌△C`GF,即FC’=DE=a,FG=GE;由tan∠M=![]() ,即tan∠MBC=
,即tan∠MBC=![]() ,可得BC=
,可得BC=![]() =2(7+
=2(7+![]() )=14+2
)=14+2![]() ;又由
;又由![]() =
=![]() =FM,可得14+2
=FM,可得14+2![]() -a=
-a=![]() +7+2a,解得a=
+7+2a,解得a=![]() ;则CE=7+
;则CE=7+![]() =
=![]() ,DE=
,DE=![]() ,故AB=CD=4;又由AB∥CD,有△AHB∽△CEH,可得
,故AB=CD=4;又由AB∥CD,有△AHB∽△CEH,可得![]() ,即BH=
,即BH=![]() BE;设CE=
BE;设CE=![]() =b,则BC=2b,由勾股定理可得BE=
=b,则BC=2b,由勾股定理可得BE=![]()
![]() ,然后代入BH=
,然后代入BH=![]() BE即可解答.
BE即可解答.
解:延长BE、AD相交于M,
∵矩形ABCD
∴AM∥BC
∴∠M=∠MBC,
∵∠M =∠MBF
∴∠M=∠MBF
∴BF=FM
∵![]() ,
,
∴DM=2DE;
设DE=a(a>0),
∵C`G=DG=7
∴GE=![]() ,
,![]() =7+
=7+![]() ,
,
∵将![]() 沿
沿![]() 折叠得到
折叠得到![]()
∴CE=![]() =7+
=7+![]() ,BC=
,BC=![]() ;
;
∵矩形ABCD
∴AM∥BC,AB∥CD,AB=CD, ∠D=∠D`=90°,
∴∠MBC=∠M
∵在△DGE和△FC`G中,∠D=∠D`=90°,∠C`GF=∠EGD,C`G=DG=7
∴△DGE≌△FC`G,
∴FC’=DE=a,FG=GE
∵∠MBC=∠M
∴tan∠M=![]() ,即tan∠MBC=
,即tan∠MBC=![]() ,
,
∴ BC=![]() =2(7+
=2(7+![]() )=14+2
)=14+2![]()
又∵![]() =
=![]() =FM,
=FM,
∴14+2![]() -a=
-a=![]() +7+2a,解得a=
+7+2a,解得a=![]() ;
;
∴ CE=7+![]() =
=![]() ,DE=a=
,DE=a=![]() ,
,
∴ AB=CD=4;
又∵AB∥CD,
∴△AHB∽△CEH,可得![]() ,即BH=
,即BH=![]() BE;
BE;
设CE=![]() =b,则BC=2b,由勾股定理可得BE=
=b,则BC=2b,由勾股定理可得BE=![]()
![]() ,
,
∴BH=![]() BE=
BE=![]() ×
×![]() =9
=9![]() .
.
故答案为9![]() .
.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,AC=2BC=4,点P为AB边中点,点E为AC边上不与端点重合的一动点,将△ADP沿着直线PD折叠得△PDE,若DE⊥AB,则AD的长度为_____ .
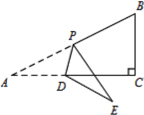
查看答案和解析>>
科目:初中数学 来源: 题型:
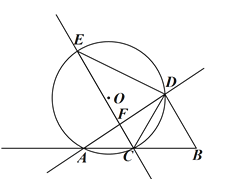
【题目】如图,AB=4,C为射线BA上一动点,以BC为边向上作正三角形BCD,⊙O过A、C、D三点,E为⊙O上一点,满足AD=ED,直线CE交直线AD于F.
(1)求证:CE∥BD;
(2)设CF=a,若C在线段AB上运动.
①求点E运动的路径长;
②求a的范围;
(3)若AC=1,求 tan∠DEC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
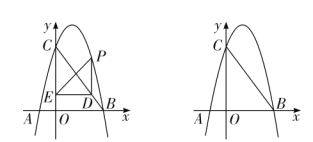
(1)求抛物线的解析式;
(2)点![]() 是抛物线上一点,设
是抛物线上一点,设![]() 点的横坐标为
点的横坐标为![]() .
.
①当点![]() 在第一象限时,过点
在第一象限时,过点![]() 作
作![]() 轴,交
轴,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() ,当
,当![]() 和
和![]() 相似时,求点
相似时,求点![]() 的坐标;
的坐标;
②请直接写出使![]() 的点
的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料69千克,乙种原料52千克,现计划用这两种原料生产A,B两种型号的产品共80件,已知每件A型号产品需要甲种原料0.6千克,乙种原料0.9千克;每件B型号产品需要甲种原料1.1千克,乙种原料0.4千克.请解答下列问题:
(1)该工厂有哪几种生产方案?
(2)在这批产品全部售出的条件下,若1件A型号产品获利35元,1件B型号产品获利25元,(1)中哪种方案获利最大?最大利润是多少?
(3)在(2)的条件下,工厂决定将所有利润的25%全部用于再次购进甲、乙两种原料,要求每种原料至少购进4千克,且购进每种原料的数量均为整数.若甲种原料每千克40元,乙种原料每千克60元,请直接写出购买甲、乙两种原料之和最多的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为原点,直线
为原点,直线![]() (
(![]() 为常数,且
为常数,且![]() )经过点
)经过点![]() ,交
,交![]() 轴于点
轴于点![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]()
![]() 求
求![]() 的值;
的值;
![]() 过点
过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() ,且
,且![]() 在线段
在线段![]() 上分别取点
上分别取点![]() 使得
使得![]() ,连接
,连接![]() ,设点
,设点![]() 的纵坐标为
的纵坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式(不要求写出自变量
之间的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
![]() 在(2)的条件下,连接
在(2)的条件下,连接![]() ,当
,当![]() 时,点
时,点![]() 在线段
在线段![]() 上,连接
上,连接![]() 且
且![]() .求
.求![]() 的值.
的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寿春路桥(如图①)横跨合肥市母亲河﹣南淝河,它位于合肥市东西交通主干道寿春路上,建成于1987年年底,为中承式钢筋砼(tong)拱桥,桥的上部结构为2个钢筋混凝土半月形拱肋,如图②是桥拱肋的简化示意图,其中拱宽(弦AB)约100米.
(1)在图②中,请你用尺规作图的方法首先找出弧AB所在圆的圆心O,然后确定弧AB、弦AB的中点C、D.(不要写作法,但保留作图痕迹)
(2)在图②中,若∠AOB=80°,求该拱桥高CD约为多少米?(结果精确到0.1米,参考数据:sin50°≈0.77,cos50°≈0.6,tan50°≈1.19)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:
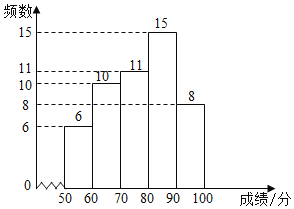
b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四位“抗疫”英雄(依次标记为![]() 、
、![]() 、
、![]() 、
、![]() ).为了让同学们了解他们的英雄事迹,张老师设计了如下活动:取四张完全相同的卡片,分别在正面写上
).为了让同学们了解他们的英雄事迹,张老师设计了如下活动:取四张完全相同的卡片,分别在正面写上![]() 、
、![]() 、
、![]() 、
、![]() 四个标号,然后背面朝上放置,搅匀后请一位同学从中随机抽取一张,记下标号后放回,要求大家依据抽到标号所对应的人物查找相应“抗疫”英雄资料.
四个标号,然后背面朝上放置,搅匀后请一位同学从中随机抽取一张,记下标号后放回,要求大家依据抽到标号所对应的人物查找相应“抗疫”英雄资料.
(1)班长在这四种卡片中随机抽到标号为![]() 的概率为___________;
的概率为___________;
(2)用树状图或列表法求小明和小亮两位同学抽到的卡片是不同“抗疫”英雄标号的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com