
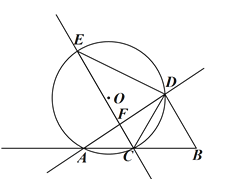
【题目】如图,AB=4,C为射线BA上一动点,以BC为边向上作正三角形BCD,⊙O过A、C、D三点,E为⊙O上一点,满足AD=ED,直线CE交直线AD于F.
(1)求证:CE∥BD;
(2)设CF=a,若C在线段AB上运动.
①求点E运动的路径长;
②求a的范围;
(3)若AC=1,求 tan∠DEC.
【答案】(1)证明见解析;(2)①4;②0≤a≤1;(3)![]() 或
或![]() ;
;
【解析】
(1)连接AE,证△ADE为等边三角形即可得到∠ECD=∠CDB=60°,则有CE∥BD.
(2) ①首先分析E点的运动轨迹是在于AB平行且距离为2![]() 的直线上,再进行计算;
的直线上,再进行计算;
②设CB的长为x(0<x<4),通过证明![]() ,得到用含x的式子表示a,从而求出a的取值范围.
,得到用含x的式子表示a,从而求出a的取值范围.
(3)分两种情况讨论:点C在线段AB上和在A点的左边两种情况分别进行计算求解.
解:(1)连接AE
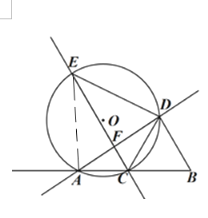
∵三角形BCD是等边三角形,
∴∠B=∠BCD=∠BDC=60°.
∵四边形ACDE是圆O的内接四边形,
∴∠AED+∠ACD=180°.
又∵∠ACD+∠BCD=180°,
∴∠AED=∠BCD=60°.
∵AD=AE,
∴三角形ADE是等边三角形.
∴∠EAD=60°,
∴∠EAD=∠ECD=∠CDB=60°.
∴CE∥BD;
(2) ①∵∠EDA=∠CDB=60°,
∴∠EDA+∠ADC=∠CDB+∠ADC,即∠EDC=∠ADB.
又∵ED=AD,CD=DB,
∴![]() .
.
∴EC=AB=4.
过点E作EG⊥AB于点G,在直角三角形CFE中,∠ECA=60°,∴EG=![]() EC=2
EC=2![]()
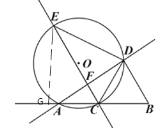
∴点E的运动轨迹为于AB平行且距离为2![]() 的直线上.
的直线上.
所以点C在A时,得到点E1, 点C在B时,得到点E2,∴四边形E1ACE2是平行四边形,
所以E1E2=AB=4.
∴E的运动路径长为4.
②设CB的长为x(0<x<4),则AC=4-x,BD=CB=x.
∵CE∥BD,
∴![]()
∴![]() =
=![]() ,∴
,∴![]() =
=![]() .
.
∴a=-![]() +x=-
+x=-![]() (x-2)2+1.
(x-2)2+1.
当x=2时,a有最大值为1;
当x=0时,a有最小值0.
∴0≤a≤1.
(3)当C在AB之间时,过点D作DH⊥AB与点H,则AC=1,BC=BD=3.
∴BH=![]() BC=
BC=![]() ,DH=
,DH=![]() BD=
BD=![]() .
.
∴AH=AB-BH=![]() .
.
∴tan∠DEC=tan∠DAH=![]() =
=![]() .
.
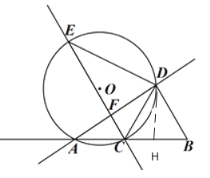
当C在A的左边时,同理可以求得tan∠DEC=tan∠DAH=![]() .
.
∴tan∠DEC的值为![]() 或
或![]() ;
;


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
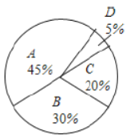
【题目】根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )

A.扇形统计图能反映各部分在总体中所占的百分比
B.每天阅读30分钟以上的居民家庭孩子超过50%
C.每天阅读1小时以上的居民家庭孩子占20%
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升学生的数学素养,某学校开展了“数学素养”竞赛活动.九年级![]() 名学生参加了竞赛,结果所有学生成绩都不低于
名学生参加了竞赛,结果所有学生成绩都不低于![]() 分(满分
分(满分![]() 分).为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表,根据表中所给信息,解答下列问题:
分).为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表,根据表中所给信息,解答下列问题:
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
![]() 表中
表中![]() ___ _ _ ,
___ _ _ ,![]() _;
_;
![]() 这组数据的中位数落在_____ _范围内;
这组数据的中位数落在_____ _范围内;
![]() 若成绩不小于
若成绩不小于![]() 分为优秀,请估计九年级大约有多少名学生获得优秀成绩?
分为优秀,请估计九年级大约有多少名学生获得优秀成绩?
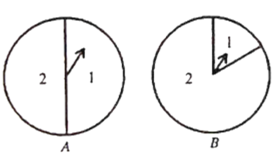
![]() 竞赛中有这样一道题目: 如图,有两个转盘
竞赛中有这样一道题目: 如图,有两个转盘![]() 在每个转盘各自的两个扇形区域中分别标有数字1,2,分别转动转盘
在每个转盘各自的两个扇形区域中分别标有数字1,2,分别转动转盘![]() 当转盘停止转动时,若事件“指针都落在标有数字
当转盘停止转动时,若事件“指针都落在标有数字![]() 的扇形区域内”概率是
的扇形区域内”概率是![]() ,则转盘
,则转盘![]() 中标有数字
中标有数字![]() 的扇形的圆心角的度数是 .
的扇形的圆心角的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
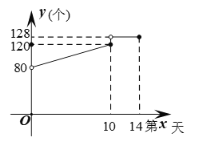
【题目】某厂家接到一批特殊产品的生产订单,客户要求在两周内完成生产,并商定这批产品的出厂价为每个16元.受市场影响,制造这批产品的某种原材料成本价持续上涨,设第x天(1≤x≤14,且x为整数)每个产品的成本为m元,m与x之间的函数关系为m=![]() x+8.订单完成后,经统计发现工人王师傅第x天生产的产品个数y与x满足如图所示的函数关系:
x+8.订单完成后,经统计发现工人王师傅第x天生产的产品个数y与x满足如图所示的函数关系:
(1)写出y与x之间的函数关系式及自变量x的取值范围;
(2)设王师傅第x天创造的产品利润为W元,问王师傅第几天创造的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y = x2 – 2 m x – 2m – 2与直线y =-x-2 交于C,D两点,将抛物线在C、D两点之间的部分(不含C、D)上恰有两个点的横坐标为整数,则m的取值范围为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是抛物线的顶点,过点
是抛物线的顶点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.
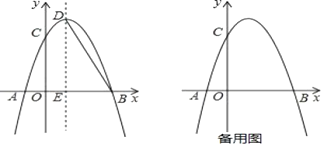
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)点![]() 是抛物线上的动点,当
是抛物线上的动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)若点![]() 是
是![]() 轴上方抛物线上的动点,以
轴上方抛物线上的动点,以![]() 为边作正方形
为边作正方形![]() ,随着点
,随着点![]() 的运动,正方形的大小、位置也随着改变,当顶点
的运动,正方形的大小、位置也随着改变,当顶点![]() 或
或![]() 恰好落在
恰好落在![]() 轴上时,请直接写出点
轴上时,请直接写出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校为了了解图书漂流的开展情况,随机抽取部分学生进行了问卷调查,选项![]() :阅读漂流图书
:阅读漂流图书![]() 本及以上;选项
本及以上;选项![]() :阅读漂流图书
:阅读漂流图书![]() 本;选项
本;选项![]() :阅读漂流图书
:阅读漂流图书![]() 本;选项
本;选项![]() :没有阅读漂流图书,只能从中选择一个选项进行回答.收集整理问卷调查的情况,把结果绘制成如下不完整的统计图:
:没有阅读漂流图书,只能从中选择一个选项进行回答.收集整理问卷调查的情况,把结果绘制成如下不完整的统计图:
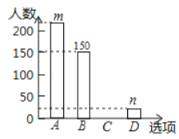
(1)此次抽样调查了_______名学生;
(2)补全条形统计图;
(3)扇形统计图![]() 选项圆心角的度数是_______;
选项圆心角的度数是_______;
(4)该校有![]() 名学生,估计全校阅读过漂流图书的学生约有多少名?
名学生,估计全校阅读过漂流图书的学生约有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com