
【题目】在平面直角坐标系xOy中,抛物线y = x2 – 2 m x – 2m – 2与直线y =-x-2 交于C,D两点,将抛物线在C、D两点之间的部分(不含C、D)上恰有两个点的横坐标为整数,则m的取值范围为______.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
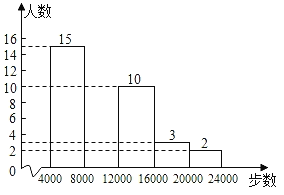
【题目】现如今”微信运动“被越来越多的人关注和喜爱,某数学兴趣小组随机调查了该校50名教师某日“微信运动“中的行走步数情况,并将统计的数据绘制成了如下两幅不完整的统计图表.请根据以上信息,解答下列问题:
(1)求出a,b,c,d的值,并补全频数分布直方图.
(2)本市约有58000名教师,用调查的样本数据估计日行步数超过12000步(包含12000步)的教师有多少名?
(3)若在被调查的50名教师中.选取日行步数超过16000步(包含16000步)的两名教师与大家分享心得,求被选取的两名教师的日行走步数恰好都在20000步(包含20000步)以上的概率.
步数(x) | 频数 | 频率 |
0≤x<4000 | a | 0.16 |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | b | 0.24 |
12000≤x<16000 | 10 | c |
16000≤x<20000 | 3 | 0.06 |
2000≤x<24000 | 2 | d |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学疫情期间为了切实抓好“停课不停学”活动,借助某软件平台随机抽取了该校部分学生的在线学习时间,并将结果绘制成如下两幅不完整的统计图.

请你根据以上信息回答下列问题
(1)本次调查的人数为 , 学习时间为7小时的所对的圆心角为 ;
(2)补全频数分布直方图;
(3)若全校共有学生1800人,估计有多少学生在线学习时间不低于8个小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,经过点B(1,0)的抛物线![]() 与y轴交于点C,其顶点为点G,过点C作y轴的垂线交抛物线对称轴于点D,线段CO上有一动点M,连接DM、DG.
与y轴交于点C,其顶点为点G,过点C作y轴的垂线交抛物线对称轴于点D,线段CO上有一动点M,连接DM、DG.
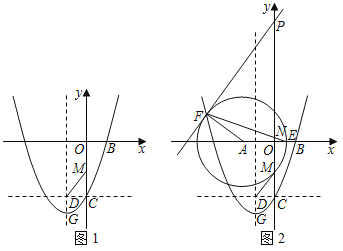
(1)求抛物线的表达式;
(2)求![]() 的最小值以及相应的点M的坐标;
的最小值以及相应的点M的坐标;
(3)如图2,在(2)的条件下,以点A(﹣2,0)为圆心,以AM长为半径作圆交x轴正半轴于点E.在y轴正半轴上有一动点P,直线PF与⊙A相切于点F,连接EF交y轴于点N,当PF∥BM时,求PN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
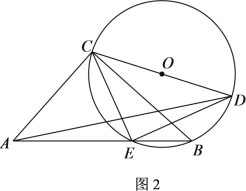
【题目】如图1,点E为△ABC边AB上的一点,⊙O为△BCE的外接圆,点D为![]() 上任意一点.若AE=AC=2n,BC=n2-1,BE=n2-2n+1 .(n≥2,且n为正整数) .
上任意一点.若AE=AC=2n,BC=n2-1,BE=n2-2n+1 .(n≥2,且n为正整数) .
(1)求证:∠CAE+∠CDE=90°;
(2)①如图2,当CD过圆心O时,①将△ACD绕点A顺时针旋转得△AEF,连接DF,请补全图形,猜想CD、DE、DF之间的数量关系,并证明你的猜想;②若n=3,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
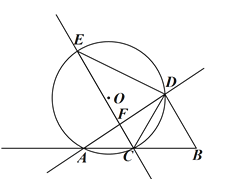
【题目】如图,AB=4,C为射线BA上一动点,以BC为边向上作正三角形BCD,⊙O过A、C、D三点,E为⊙O上一点,满足AD=ED,直线CE交直线AD于F.
(1)求证:CE∥BD;
(2)设CF=a,若C在线段AB上运动.
①求点E运动的路径长;
②求a的范围;
(3)若AC=1,求 tan∠DEC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收2元印刷费,另收1000元的制版费;乙印刷厂提出:每份材料收3元印刷费,不收制版费.
(1)分别写出两个印刷厂的收费![]() ,
,![]() (元)与印制数量
(元)与印制数量![]() (份)之间的关系式(不用写出自变量的取值范围);
(份)之间的关系式(不用写出自变量的取值范围);
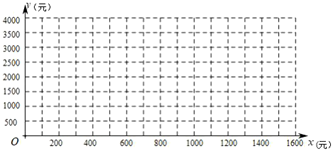
(2)在同一坐标系内画出它们的图象,并求出当印制多少份宣传材料,两个印刷厂的印制费用相同?此时费用为多少?
(3)结合图象回答:在印刷品数量相同的情况下选哪家印刷厂印制省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料69千克,乙种原料52千克,现计划用这两种原料生产A,B两种型号的产品共80件,已知每件A型号产品需要甲种原料0.6千克,乙种原料0.9千克;每件B型号产品需要甲种原料1.1千克,乙种原料0.4千克.请解答下列问题:
(1)该工厂有哪几种生产方案?
(2)在这批产品全部售出的条件下,若1件A型号产品获利35元,1件B型号产品获利25元,(1)中哪种方案获利最大?最大利润是多少?
(3)在(2)的条件下,工厂决定将所有利润的25%全部用于再次购进甲、乙两种原料,要求每种原料至少购进4千克,且购进每种原料的数量均为整数.若甲种原料每千克40元,乙种原料每千克60元,请直接写出购买甲、乙两种原料之和最多的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com