
【题目】如图,Rt△ACB中,∠ACB=90°,AC=2BC=4,点P为AB边中点,点E为AC边上不与端点重合的一动点,将△ADP沿着直线PD折叠得△PDE,若DE⊥AB,则AD的长度为_____ .
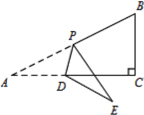
【答案】![]() 或
或![]()
【解析】
分类讨论:①当点E在直线AC上方时,设DM=x,先证明△AMD∽△ACB,得出AM=2x,勾股定理表达出AD及ME,求出AB,表达出MP,根据tan∠E=![]() =
=![]() 列出方程解答;②当点E在直线AC上方时,设DN=y,表达出AD,AN,以及PN,EN,根据tan∠E=
列出方程解答;②当点E在直线AC上方时,设DN=y,表达出AD,AN,以及PN,EN,根据tan∠E=![]() =
=![]() 列出方程解答即可.
列出方程解答即可.
分类讨论如下:①当点E在直线AC上方时,如图1,设DM=x.
∵∠A=∠A,∠AMD=∠C,
∴△AMD∽△ACB,∴AM:MD=AC:BC=2,
∴AM=2x,
在Rt△AMD中,AM=2x,DM=x,
∴AD=![]() =
=![]() ,
,
∴DE=AD=![]() ,
,
∴ME=![]() ,
,
在Rt△ACB中,AC=4,BC=2,
∴AB=![]() =
=![]() ,
,
∴AP=![]() AB=
AB=![]() ,
,
∴MP=![]()
∵∠E=∠A,
∴tan∠E=![]() =
=![]() ,即:
,即: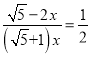 ,解得:
,解得:![]() ,
,
∴AD=![]() =
=![]() ;
;
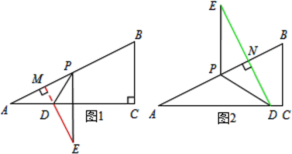
②当点E在直线AC上方时,如图2,设DN=y.
∵DN=y,同①可得AD=![]() ,AN=2y,
,AN=2y,
∵AP=![]() ,
,
∴PN=![]() ,EN=
,EN=![]() ,
,
∵tan∠E=![]() =
=![]() ,
,
∴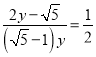 ,解得:
,解得:![]() ,∴AD=
,∴AD=![]() =
=![]() ;
;
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
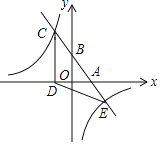
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )

A.扇形统计图能反映各部分在总体中所占的百分比
B.每天阅读30分钟以上的居民家庭孩子超过50%
C.每天阅读1小时以上的居民家庭孩子占20%
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探究证明】
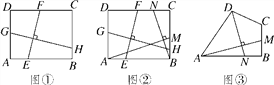
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图①,在矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: ![]() ;
;
【结论应用】
(2)如图②,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若![]() ,则
,则![]() 的值为 ;
的值为 ;
【联系拓展】
(3)如图③,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的3月15日是“国际消费者权益日”,许多家居商城都会利用这个契机进行打折促销活动.甲卖家的某款沙发每套成本为5000元,在标价8000元的基础上打9折销售.
(1)现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于20%?
(2)据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售相同的沙发,其成本、标价与甲卖家一致,以前每周可售出8套,现乙卖家先将标价提高![]() ,再大幅降价
,再大幅降价![]() 元,使得这款沙发在3月15日那一天卖出的数量就比原来一周卖出的数量增加了
元,使得这款沙发在3月15日那一天卖出的数量就比原来一周卖出的数量增加了![]() ,这样一天的利润达到了50000元,求
,这样一天的利润达到了50000元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接体育理化加试,九(2)班同学到某体育用品商店采购训练用球,已知购买3个A品牌足球和2个B品牌足球需付210元;购买2个A品牌足球和1个B品牌足球需付费130元.(优惠措施见海报)巨惠来袭(解释权归本店所有)
A品牌 | B品牌 |
|
|
单品数量低于40个不优惠,高于40个 享8折优惠 | 单品数量低于40个不优惠,高于40个 享9折优惠 |
(1)求A,B两品牌足球的单价各为多少元?
(2)为享受优惠,同学们决定购买一次性购买足球60个,若要求A品牌足球的数量不低于B品牌足球数量的3倍,请你设计一种付费最少的方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升学生的数学素养,某学校开展了“数学素养”竞赛活动.九年级![]() 名学生参加了竞赛,结果所有学生成绩都不低于
名学生参加了竞赛,结果所有学生成绩都不低于![]() 分(满分
分(满分![]() 分).为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表,根据表中所给信息,解答下列问题:
分).为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表,根据表中所给信息,解答下列问题:
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
![]() 表中
表中![]() ___ _ _ ,
___ _ _ ,![]() _;
_;
![]() 这组数据的中位数落在_____ _范围内;
这组数据的中位数落在_____ _范围内;
![]() 若成绩不小于
若成绩不小于![]() 分为优秀,请估计九年级大约有多少名学生获得优秀成绩?
分为优秀,请估计九年级大约有多少名学生获得优秀成绩?
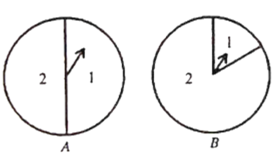
![]() 竞赛中有这样一道题目: 如图,有两个转盘
竞赛中有这样一道题目: 如图,有两个转盘![]() 在每个转盘各自的两个扇形区域中分别标有数字1,2,分别转动转盘
在每个转盘各自的两个扇形区域中分别标有数字1,2,分别转动转盘![]() 当转盘停止转动时,若事件“指针都落在标有数字
当转盘停止转动时,若事件“指针都落在标有数字![]() 的扇形区域内”概率是
的扇形区域内”概率是![]() ,则转盘
,则转盘![]() 中标有数字
中标有数字![]() 的扇形的圆心角的度数是 .
的扇形的圆心角的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
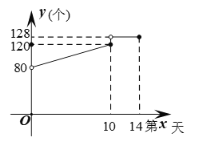
【题目】某厂家接到一批特殊产品的生产订单,客户要求在两周内完成生产,并商定这批产品的出厂价为每个16元.受市场影响,制造这批产品的某种原材料成本价持续上涨,设第x天(1≤x≤14,且x为整数)每个产品的成本为m元,m与x之间的函数关系为m=![]() x+8.订单完成后,经统计发现工人王师傅第x天生产的产品个数y与x满足如图所示的函数关系:
x+8.订单完成后,经统计发现工人王师傅第x天生产的产品个数y与x满足如图所示的函数关系:
(1)写出y与x之间的函数关系式及自变量x的取值范围;
(2)设王师傅第x天创造的产品利润为W元,问王师傅第几天创造的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com