
【题目】如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E.将△BDE沿直线DE折叠,得到△B′DE,若B′D,B′E分别交AC于点F,G,连接OF,OG,则下列判断错误的是( )
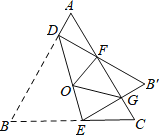
A. △ADF≌△CGE
B. △B′FG的周长是一个定值
C. 四边形FOEC的面积是一个定值
D. 四边形OGB'F的面积是一个定值
【答案】D
【解析】A、根据等边三角形ABC的外心的性质可知:AO平分∠BAC,根据角平分线的定理和逆定理得:FO平分∠DFG,由外角的性质可证明∠DOF=60°,同理可得∠EOG=60°,∠FOG=60°=∠DOF=∠EOG,可证明△DOF≌△GOF≌△GOE,△OAD≌△OCG,△OAF≌△OCE,可得AD=CG,AF=CE,从而得△ADF≌△CGE;
B、根据△DOF≌△GOF≌△GOE,得DF=GF=GE,所以△ADF≌△B'GF≌△CGE,可得结论;
C、根据S四边形FOEC=S△OCF+S△OCE,依次换成面积相等的三角形,可得结论为:S△AOC=![]() S△ABC(定值),可作判断;
S△ABC(定值),可作判断;
D、方法同C,将S四边形OGB'F=S△OAC-S△OFG,根据S△OFG=![]() FGOH,FG变化,故△OFG的面积变化,从而四边形OGB'F的面积也变化,可作判断.
FGOH,FG变化,故△OFG的面积变化,从而四边形OGB'F的面积也变化,可作判断.
A、连接OA、OC,
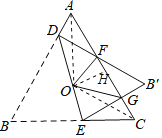
∵点O是等边三角形ABC的外心,
∴AO平分∠BAC,
∴点O到AB、AC的距离相等,
由折叠得:DO平分∠BDB',
∴点O到AB、DB'的距离相等,
∴点O到DB'、AC的距离相等,
∴FO平分∠DFG,
∠DFO=∠OFG=![]() (∠FAD+∠ADF),
(∠FAD+∠ADF),
由折叠得:∠BDE=∠ODF=![]() (∠DAF+∠AFD),
(∠DAF+∠AFD),
∴∠OFD+∠ODF=![]() (∠FAD+∠ADF+∠DAF+∠AFD)=120°,
(∠FAD+∠ADF+∠DAF+∠AFD)=120°,
∴∠DOF=60°,
同理可得∠EOG=60°,
∴∠FOG=60°=∠DOF=∠EOG,
∴△DOF≌△GOF≌△GOE,
∴OD=OG,OE=OF,
∠OGF=∠ODF=∠ODB,∠OFG=∠OEG=∠OEB,
∴△OAD≌△OCG,△OAF≌△OCE,
∴AD=CG,AF=CE,
∴△ADF≌△CGE,
故选项A正确;
B、∵△DOF≌△GOF≌△GOE,
∴DF=GF=GE,
∴△ADF≌△B'GF≌△CGE,
∴B'G=AD,
∴△B'FG的周长=FG+B'F+B'G=FG+AF+CG=AC(定值),
故选项B正确;
C、S四边形FOEC=S△OCF+S△OCE=S△OCF+S△OAF=S△AOC=![]() S△ABC(定值),
S△ABC(定值),
故选项C正确;
D、S四边形OGB'F=S△OFG+S△B'GF=S△OFD+△ADF=S四边形OFAD=S△OAD+S△OAF=S△OCG+S△OAF=S△OAC-S△OFG,
过O作OH⊥AC于H,
∴S△OFG=![]() FGOH,
FGOH,
由于OH是定值,FG变化,故△OFG的面积变化,从而四边形OGB'F的面积也变化,
故选项D不一定正确;
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() ,线段
,线段![]() 上有动点
上有动点![]() ,过
,过![]() 作直线
作直线![]() 交
交![]() 边于点
边于点![]() ,并使得
,并使得![]() .
.
![]() 当
当![]() 与
与![]() 重合时,求
重合时,求![]() 的长;
的长;
![]() 在直线
在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 是等腰直角三角形?若存在,求出
是等腰直角三角形?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形![]() 的边长为
的边长为![]() 厘米,对角线
厘米,对角线![]() 上的两个动点
上的两个动点![]() ,
,![]() .点
.点![]() 从点
从点![]() ,点
,点![]() 从点
从点![]() 同时出发,沿对角线以
同时出发,沿对角线以![]() 厘米/秒的相同速度运动,过
厘米/秒的相同速度运动,过![]() 作
作![]() 交
交![]() 的直角边于
的直角边于![]() ,过
,过![]() 作
作![]() 交
交![]() 的直角边于
的直角边于![]() ,连接
,连接![]() ,
,![]() .设
.设![]() 、
、![]() 、
、![]() 、
、![]() 围成的图形面积为
围成的图形面积为![]() ,
,![]() ,
,![]() ,
,![]() 围成的图形面积为
围成的图形面积为![]() (这里规定:线段的面积为
(这里规定:线段的面积为![]() 到达
到达![]() ,
,![]() 到达
到达![]() 停止.若
停止.若![]() 的运动时间为
的运动时间为![]() 秒,解答下列问题:
秒,解答下列问题:

![]() 如图,判断四边形
如图,判断四边形![]() 是什么四边形,并证明;
是什么四边形,并证明;
![]() 当
当![]() 时,求
时,求![]() 为何值时,
为何值时,![]() ;
;
![]() 若
若![]() 是
是![]() 与
与![]() 的和,试用
的和,试用![]() 的代数式表示
的代数式表示![]() .(如图为备用图)
.(如图为备用图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有2个信封,每个信封内各装有四张卡片,其中一个信封内的四张卡片上分别写有1、2、3、4四个数,另一个信封内的四张卡片分别写有5、6、7、8四个数,甲、乙两人商定了一个游戏,规则是:从这两个信封中各随机抽取一张卡片,然后把卡片上的两个数相乘,如果得到的积大于20,则甲获胜,否则乙获胜.
(1)请你通过列表(或画树状图)计算甲获胜的概率
(2)你认为这个游戏公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB=12,AC⊥AB,BD⊥AB,AC=BD=8。点P在线段AB上以每秒2个单位的速度由点A向点B运动,同时,点Q在线段BD上由B点向点D运动。它们的运动时间为t(s).


(1)若点Q的运动速度与点P的运动速度相等,当t=2时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图2,将图1中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变。设点Q的运动速度为每秒x个单位,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x,t的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC=8,∠BAC=90,直线l与以AB为直径的⊙O相切于点B,点D是直线l上任意一动点,连结DA交⊙O点E.
(1)当点D在AB上方且BD=6时,求AE的长;
(2)当CE恰好与⊙O相切时,求BD的长为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D.CD=3,则BC的长为( )

A. 6 B. 9 C. 6![]() D. 3
D. 3![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com