
【题目】如图,一副三角尺△ABC与△ADE的两条斜边在一条直线上,直尺的一边GF∥AC,则∠DFG的度数为_____________.
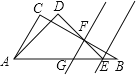
【答案】105°
【解析】
解法一:利用平行线的性质定理∠CFG=180°-∠C =90°,利用等角的余角相等得出∠CFD=∠CAD=15°,它们之和即为∠DFG;
解法二:利用平行线的性质定理可求出∠FGE=∠CAB=60°,再利用三角形的外角和可求出∠FGE=∠FGE+∠DEA=105°.
解法一:∵GF∥AC,∠C=90°,
∴∠CFG=180°-90°=90°,
又∵AD,CF交于一点,∠C=∠D,
∴∠CAD=∠CFD=60°-45°=15°,
∴∠DFG=∠CFD+∠CFG=15°+90°=105°.
解法二:∵GF∥AC,∠CAB=60°,
∴∠FGE=60°,
又∵∠DFG是△EFG的外角,∠FEG=45°,
∴∠DFG=∠FGE+∠FEG=60°+45°=105°,
故答案为:105°.


科目:初中数学 来源: 题型:
【题目】某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的![]() 倍,购进数量比第一次少了30支.
倍,购进数量比第一次少了30支.
(1)求第一次每支铅笔的进价是多少元?
(2)若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元,问每支售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).

(1)当t为何值时,四边形PQDC是平行四边形
(2)当t为何值时,以C,D,Q,P为顶点的梯形面积等于60cm2?
(3)是否存在点P,使△PQD是等腰三角形?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架梯子的长度为25米,斜靠在墙上,梯子低部离墙底端为7米.
(1)这个梯子顶端离地面有 米;
(2)如果梯子的顶端下滑了4米,那么梯子的底部在水平方向滑动了几米?

查看答案和解析>>
科目:初中数学 来源: 题型:
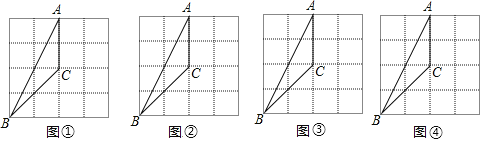
【题目】如图,在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)在图1中,画出一个与△ABC成中心对称的格点三角形;
(2)在图2中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;
(3)在图3中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形;
(4)在图4中,画出所有格点△BCD,使△BCD为等腰直角三角形,且S△BCD=4.
查看答案和解析>>
科目:初中数学 来源: 题型:
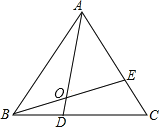
【题目】如图,点D、E分别是等边三角形ABC的边BC、AC上的点,连接AD、BE交于点O,且△ABD≌△BCE.
(1)若AB=3,AE=2,则BD= ;
(2)若∠CBE=15°,则∠AOE= ;
(3)若∠BAD=a,猜想∠AOE的度数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某酒厂每天生产A,B两种品牌的白酒共600瓶,A,B两种品牌的白酒每瓶的成本和利润如下表:设每天生产A种品牌白酒x瓶,每天获利y元.
(1)请写出y关于x的函数关系式;
(2)如果该酒厂每天至少投入成本26400元,那么每天至少获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛是古代的一种容量位),1个大桶加上5个小桶可以盛酒2斛。
(1)1个大桶、1个小桶分别可以盛酒多少斛?
(2)盛酒16斛,需要大桶、小桶各多少?(写出两种方案即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com