
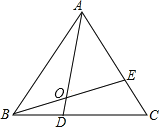
【题目】如图,点D、E分别是等边三角形ABC的边BC、AC上的点,连接AD、BE交于点O,且△ABD≌△BCE.
(1)若AB=3,AE=2,则BD= ;
(2)若∠CBE=15°,则∠AOE= ;
(3)若∠BAD=a,猜想∠AOE的度数,并说明理由.
【答案】(1)BD=1;(2)60°;(3)∠AOE =60°.
【解析】
(1)根据等边三角形的性质求出AC,得到EC,根据全等三角形的性质解答;
(2)根据全等三角形的性质得到∠BAD=∠CBE=15°,根据三角形的外角性质计算即可;
(3)仿照(2)的作法解答.
解:(1)∵△ABC是等边三角形,
∴AC=AB=3,
∴EC=AC-AE=1,
∵△ABD≌△BCE,
∴BD=EC=1,
故答案为:1;
(2)∵△ABD≌△BCE,
∴∠BAD=∠CBE=15°,
∵∠CBE=15°,
∴∠ABO=45°,
∴∠AOE=∠BAD+∠ABO=60°,
故答案为:60°;
(3)由(2)得,∠BAD=∠CBE,
∵∠ABO+∠CBE=60°,
∴∠AOE=∠BAD+∠ABO=60°.


科目:初中数学 来源: 题型:
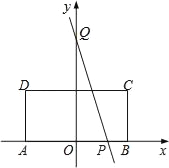
【题目】如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )
A. ![]() 或-
或-![]() B.
B. ![]() 或-
或-![]() C.
C. ![]() 或-
或-![]() D.
D. ![]() 或-
或-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣昌公司要将本公司100吨货物运往某地销售,经与春晨运输公司协商,计划租用甲、乙两种型号的汽车共6辆,用这6辆汽车一次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨.已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元;租用2辆甲型汽车和1辆乙型汽车共需费用2450元,且同一种型号汽车每辆租车费用相同.
(1)求租用一辆甲型汽车、一辆乙型汽车的费用分别是多少元?
(2)若荣昌公司计划此次租车费用不超过5000元.通过计算求出该公司有几种租车方案?请你设计出来,并求出最低的租车费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )
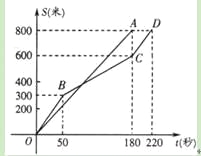
A. 小莹的速度随时间的增大而增大B. 小梅的平均速度比小莹的平均速度大
C. 在起跑后180秒时,两人相遇D. 在起跑后50秒时,小梅在小莹的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解学生对手机的依赖程度,开展了一次“学生周末手机使用时间”抽样调查,根据调查结果绘制了如下两种不完整的统计图表.
组别 | 周末手机使用时间 | 人数 |
|
| 20 |
|
|
|
|
| 22 |
|
| 10 |
|
| 8 |
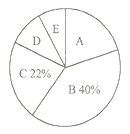
请根据图表信息解答下列问题:
(1)本次抽样,共调查了 人;
(2)扇形统计图中“![]() ”所对应的圆心角的度数是/span> ;
”所对应的圆心角的度数是/span> ;
(3)估计该校2450名学生中周末手机使用时间小于2小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 两地相距6千米,甲骑自行车从
两地相距6千米,甲骑自行车从![]() 地出发前往
地出发前往![]() 地,同时乙从
地,同时乙从![]() 地出发步行前往
地出发步行前往![]() 地.
地.

(1)已知甲的速度为16千米/小时,乙的速度为4千米/小时,求两人出发几小时后甲追上乙;
(2)甲追上乙后,两人都提高了速度,但甲比乙每小时仍然多行12千米,甲到达![]() 地后立即返回,两人在
地后立即返回,两人在![]() 两地的中点处相遇,此时离甲追上乙又经过了2小时.求
两地的中点处相遇,此时离甲追上乙又经过了2小时.求![]() 两地相距多少千米.
两地相距多少千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
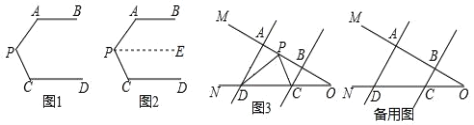
【题目】(1)如图1,AB∥CD,∠PAB=120°,∠PCD=110°,求∠APC的度数.小颖同学的解题思路是:如图2,过点P作PE∥AB,请你接着完成解答;如图3,点A、B在射线OM上,点C、D在射线ON上,AD∥BC,点P在射线OM上运动(点P与A、B、O三点不重合).
(2)当点P在线段AB上运动时,判断∠CPD与∠ADP、∠BCP之间的数量关系,并说明理由;
(3)当点P在线段AB外运动时,判断∠CPD与∠ADP、∠BCP之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com