
【题目】如图,已知![]() 两地相距6千米,甲骑自行车从
两地相距6千米,甲骑自行车从![]() 地出发前往
地出发前往![]() 地,同时乙从
地,同时乙从![]() 地出发步行前往
地出发步行前往![]() 地.
地.

(1)已知甲的速度为16千米/小时,乙的速度为4千米/小时,求两人出发几小时后甲追上乙;
(2)甲追上乙后,两人都提高了速度,但甲比乙每小时仍然多行12千米,甲到达![]() 地后立即返回,两人在
地后立即返回,两人在![]() 两地的中点处相遇,此时离甲追上乙又经过了2小时.求
两地的中点处相遇,此时离甲追上乙又经过了2小时.求![]() 两地相距多少千米.
两地相距多少千米.
【答案】(1)两人出发![]() 小时后甲追上乙;(2)
小时后甲追上乙;(2)![]() 两地相距30千米.
两地相距30千米.
【解析】
(1)设两人出发t小时后甲追上乙,根据题意就有16t﹣4t=6,解方程即可求解;
(2)可设速度提高了a千米/小时,BC段长度为x千米,两人在B、C两地的中点处相遇,则甲比乙多走的路程为BC段,于是可得方程2(16+a)﹣2(4+a)=x,解方程即可得BC段,于是可求A、C两地距离.
(1)设两人出发t小时后甲追上乙,根据题意得
16t﹣4t=6,
得t=![]() ,
,
答:两人出发![]() 小时后甲追上乙;
小时后甲追上乙;
(2)设两个人的速度提高了a千米/小时,BC段长度为x千米,根据题意有
2(16+a)﹣2(4+a)=x,
得x=24,
故BC段距离为24千米,
∴AC=AB+BC=6+24=30,
答:A、C两地相距30千米.


科目:初中数学 来源: 题型:
【题目】若a、b、c为△ABC的三边。
(1)判断代数式a![]() 2abc
2abc![]() +b
+b![]() 的值与0的大小关系,并说明理由;
的值与0的大小关系,并说明理由;
(2)满足a![]() +b
+b![]() +c
+c![]() =ab+ac+bc,试判断△ABC的形状.
=ab+ac+bc,试判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架梯子的长度为25米,斜靠在墙上,梯子低部离墙底端为7米.
(1)这个梯子顶端离地面有 米;
(2)如果梯子的顶端下滑了4米,那么梯子的底部在水平方向滑动了几米?

查看答案和解析>>
科目:初中数学 来源: 题型:
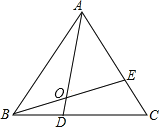
【题目】如图,点D、E分别是等边三角形ABC的边BC、AC上的点,连接AD、BE交于点O,且△ABD≌△BCE.
(1)若AB=3,AE=2,则BD= ;
(2)若∠CBE=15°,则∠AOE= ;
(3)若∠BAD=a,猜想∠AOE的度数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1所示的三棱柱,高为![]() ,底面是一个边长为
,底面是一个边长为![]() 的等边三角形.
的等边三角形.
(1)这个三棱柱有 条棱,有 个面;
(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开 条棱,需剪开棱的棱长的和的最大值为 ![]() .
.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某酒厂每天生产A,B两种品牌的白酒共600瓶,A,B两种品牌的白酒每瓶的成本和利润如下表:设每天生产A种品牌白酒x瓶,每天获利y元.
(1)请写出y关于x的函数关系式;
(2)如果该酒厂每天至少投入成本26400元,那么每天至少获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合.三角板的一边交CD于点F,另一边交CB的延长线于点G.

(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a,BC=b,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某造纸厂为了保护环境,准备购买A,B两种型号的污水处理设备共6台,用于同时治理不同成分的污水,若购买A型2台,B型3台需54万元,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水180吨,如果该企业每月的污水处理量不低于1150吨,问共有几种购买方案?请你为该企业设计一种最省钱的购买方案并求此时的购买费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
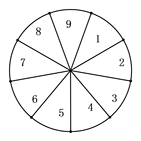
【题目】小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去等加活动:将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,
若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新特动转盘.
(1)转盘转到2的倍数的概率是多少?
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com