
【题目】若a、b、c为△ABC的三边。
(1)判断代数式a![]() 2abc
2abc![]() +b
+b![]() 的值与0的大小关系,并说明理由;
的值与0的大小关系,并说明理由;
(2)满足a![]() +b
+b![]() +c
+c![]() =ab+ac+bc,试判断△ABC的形状.
=ab+ac+bc,试判断△ABC的形状.
【答案】(1)a![]() 2abc
2abc![]() +b
+b![]() <0;(2)△ABC是等边三角形.
<0;(2)△ABC是等边三角形.
【解析】
(1)根据完全平方公式和平方差公式先将代数式进行变形,然后利用三角形三边关系即可判断.
(2)根据完全平方公式将题目所给的等式进行变形,然后利用非负性即可求出答案.
(1) a![]() 2abc
2abc![]() +b
+b![]() =(ab)
=(ab) ![]() c
c![]() =(ab+c)(abc)
=(ab+c)(abc)
∵a+c>b,a<b+c,
∴ab+c>0,abc<0,
∴a![]() 2abc
2abc![]() +b
+b![]() <0
<0
(2)∵a![]() +b
+b![]() +c
+c![]() =ab+ac+bc
=ab+ac+bc
∴2a![]() +2b
+2b![]() +2c
+2c![]() 2ab2ac2bc=0,
2ab2ac2bc=0,
∴a![]() 2ab+b
2ab+b![]() +b
+b![]() 2bc+c
2bc+c![]() +a
+a![]() 2ac+c
2ac+c![]() =0,
=0,
∴(ab) ![]() +(bc)
+(bc) ![]() +(ac)
+(ac) ![]() =0,
=0,
∴ab=0,bc=0,ac=0,
∴a=b=c,
∴△ABC是等边三角形.


科目:初中数学 来源: 题型:
【题目】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).


图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
已知:如图,四边形ABCD中,∠A=106°![]() , ∠ABC=74°
, ∠ABC=74°![]() ,BD⊥DC于点D, EF⊥DC于点F.
,BD⊥DC于点D, EF⊥DC于点F.
求证:∠1=∠2.

证明: ∵∠A=106°![]() ,∠ABC=74°
,∠ABC=74°![]() (已知)
(已知)
∴∠A+∠ABC=180°
![]() ( )
( )
∴∠1=
∵BD⊥DC,EF⊥DC (已知)
∴∠BDF=∠EFC=90°( )
∴BD∥ ( )
∴∠2= ( )
![]() (已证)
(已证)
∴∠1=∠2 ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
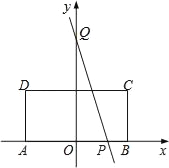
【题目】如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )
A. ![]() 或-
或-![]() B.
B. ![]() 或-
或-![]() C.
C. ![]() 或-
或-![]() D.
D. ![]() 或-
或-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点(与点
上一动点(与点![]() 不重合),
不重合),![]() 分别平分
分别平分![]() 和
和![]() ,分别交射线
,分别交射线![]() 于点
于点![]() .
.

(1)![]() ;
;![]() ;
;
(2)当点![]() 运动到某处时,
运动到某处时,![]() ,求此时
,求此时![]() 的度数.
的度数.
(3)当点![]() 运动时,
运动时,![]() :
:![]() 的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
查看答案和解析>>
科目:初中数学 来源: 题型:
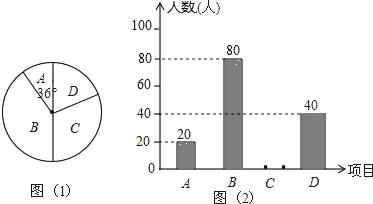
【题目】某学校为了提高学生学科能力,决定开设以下校本课程:A.文学院,B.小小数学家,C.小小外交家,D.未来科学家,为了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的小小外交家的课堂学习中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加全国英语口语大赛,求恰好同时选中甲、乙两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于频率与概率有下列几种说法:①“明天下雨的概率是90%”表示明天下雨的可能性很大;②“抛一枚硬币正面朝上的概率为![]() ”表示每抛两次就有一次正面朝上;③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖;④“抛一枚硬币正面朝上的概率为
”表示每抛两次就有一次正面朝上;③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖;④“抛一枚硬币正面朝上的概率为![]() ”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在![]() 附近,正确的说法是( )
附近,正确的说法是( )
A. ②④B. ②③C. ①④D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣昌公司要将本公司100吨货物运往某地销售,经与春晨运输公司协商,计划租用甲、乙两种型号的汽车共6辆,用这6辆汽车一次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨.已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元;租用2辆甲型汽车和1辆乙型汽车共需费用2450元,且同一种型号汽车每辆租车费用相同.
(1)求租用一辆甲型汽车、一辆乙型汽车的费用分别是多少元?
(2)若荣昌公司计划此次租车费用不超过5000元.通过计算求出该公司有几种租车方案?请你设计出来,并求出最低的租车费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 两地相距6千米,甲骑自行车从
两地相距6千米,甲骑自行车从![]() 地出发前往
地出发前往![]() 地,同时乙从
地,同时乙从![]() 地出发步行前往
地出发步行前往![]() 地.
地.

(1)已知甲的速度为16千米/小时,乙的速度为4千米/小时,求两人出发几小时后甲追上乙;
(2)甲追上乙后,两人都提高了速度,但甲比乙每小时仍然多行12千米,甲到达![]() 地后立即返回,两人在
地后立即返回,两人在![]() 两地的中点处相遇,此时离甲追上乙又经过了2小时.求
两地的中点处相遇,此时离甲追上乙又经过了2小时.求![]() 两地相距多少千米.
两地相距多少千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com