
【题目】某造纸厂为了保护环境,准备购买A,B两种型号的污水处理设备共6台,用于同时治理不同成分的污水,若购买A型2台,B型3台需54万元,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水180吨,如果该企业每月的污水处理量不低于1150吨,问共有几种购买方案?请你为该企业设计一种最省钱的购买方案并求此时的购买费用.
【答案】(1)A型污水处理设备的单价为12万元,B型污水处理设备的单价为10万元;(2)详见解析.
【解析】
(1)根据题意结合购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元分别得出等式求出答案;
(2)利用该企业每月的污水处理量不低于1150吨,得出不等式求出答案.
(1)设A型污水处理设备的单价为x万元,B型污水处理设备的单价为y万元,根据题意可得:![]() ,
,
解得:![]() .
.
答:A型污水处理设备的单价为12万元,B型污水处理设备的单价为10万元;
(2)设购进a台A型污水处理器,根据题意可得:
200a+180(6﹣a)≥1150,
解得:a≥3.5,
因为a是整数,
所以a=4,5,6,
所以6﹣a=2,1,0,
所以有3种方案:
方案一:购进4台A型污水处理设备,购进2台B型污水处理设备;
方案二:购进5台A型污水处理设备,购进1台B型污水处理设备;
方案三:购进6台A型污水处理设备,购进0台B型污水处理设备.
∵A型污水处理设备单价比B型污水处理设备单价高,
∴A型污水处理设备买越少,越省钱,
∴购进4台A型污水处理设备,购进2台B型污水处理设备最省钱.
购买的费用:4×12+2×10=68(万元).


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】荣昌公司要将本公司100吨货物运往某地销售,经与春晨运输公司协商,计划租用甲、乙两种型号的汽车共6辆,用这6辆汽车一次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨.已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元;租用2辆甲型汽车和1辆乙型汽车共需费用2450元,且同一种型号汽车每辆租车费用相同.
(1)求租用一辆甲型汽车、一辆乙型汽车的费用分别是多少元?
(2)若荣昌公司计划此次租车费用不超过5000元.通过计算求出该公司有几种租车方案?请你设计出来,并求出最低的租车费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 两地相距6千米,甲骑自行车从
两地相距6千米,甲骑自行车从![]() 地出发前往
地出发前往![]() 地,同时乙从
地,同时乙从![]() 地出发步行前往
地出发步行前往![]() 地.
地.

(1)已知甲的速度为16千米/小时,乙的速度为4千米/小时,求两人出发几小时后甲追上乙;
(2)甲追上乙后,两人都提高了速度,但甲比乙每小时仍然多行12千米,甲到达![]() 地后立即返回,两人在
地后立即返回,两人在![]() 两地的中点处相遇,此时离甲追上乙又经过了2小时.求
两地的中点处相遇,此时离甲追上乙又经过了2小时.求![]() 两地相距多少千米.
两地相距多少千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
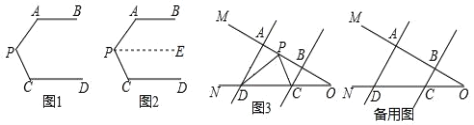
【题目】(1)如图1,AB∥CD,∠PAB=120°,∠PCD=110°,求∠APC的度数.小颖同学的解题思路是:如图2,过点P作PE∥AB,请你接着完成解答;如图3,点A、B在射线OM上,点C、D在射线ON上,AD∥BC,点P在射线OM上运动(点P与A、B、O三点不重合).
(2)当点P在线段AB上运动时,判断∠CPD与∠ADP、∠BCP之间的数量关系,并说明理由;
(3)当点P在线段AB外运动时,判断∠CPD与∠ADP、∠BCP之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
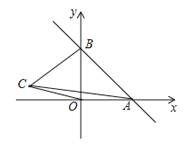
【题目】如图,一次函数y=kx+b的图象分别与x轴,y轴的正半轴分別交于点A,B,AB=2![]() ,∠OAB=45°
,∠OAB=45°
(1)求一次函数的解析式;
(2)如果在第二象限内有一点C(a,![]() );试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
);试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
(3)在x轴上,是否存在点P,使△PAB为等腰三角形?若存在,请直接写出所有符合条件的点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
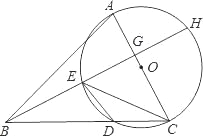
【题目】已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧![]() 上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读下文,寻找规律:
已知 x≠1 时,(1-x)(1+x)=1-x![]() ,
,
(1-x)(1+x+x![]() )=1-x
)=1-x![]() ,
,
(1-x)(1+x+x![]() +x
+x![]() )=1-x
)=1-x![]() .…
.…
观察上式,并猜想:
(1-x)(1+x+x![]() + x
+ x![]() +x
+x![]() )= ____________. (1-x)(1+x+x
)= ____________. (1-x)(1+x+x![]() +…+x
+…+x![]() )= ____________.
)= ____________.
(2) 通过以上规律,请你进行下面的探素:
①(a-b)(a+b)= ____________.
②(a-b)(a![]() +ab+b
+ab+b![]() )= ____________.
)= ____________.
③(a-b)(a![]() +a
+a![]() +ab
+ab![]() +b
+b![]() )= ____________.
)= ____________.
(3) 根据你的猜想,计算:
1+2+2![]() +…+2
+…+2![]() +2
+2![]() +2
+2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=4,AD=2,点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P、Q两点相遇时,它们同时停止运动。设Q点运动的时间为![]() (秒),在整个运动过程中,求解下面问题:
(秒),在整个运动过程中,求解下面问题:
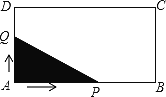
(1)当P、Q相遇时,求出![]() 的值(列方程解决问题);
的值(列方程解决问题);
(2)当△APQ的面积为![]() 时,此时t的值是_________;
时,此时t的值是_________;
(3)当△APQ为直角三角形时,直接写出相应的![]() 的值或取值范围.
的值或取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com