Question

如图，在△ABC中E是BC上的一点，EC=2EB，点D是AC的中点，AE、BD交于点F，AF=3FE．若△ABC的面积为18，给出下列命题：

①△ABE的面积为6；

②△ABF的面积和四边形DFEC的面积相等；

③点F是BD的中点；

④四边形DFEC的面积为．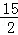

其中，正确的结论有         ．（把你认为正确的结论的序号都填上）

   

Answer 1

①③④    解：①∵△ABC的面积为18，EC=2EB，

∴△ABE的面积=18×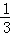=6，故①正确；

②∵EC=2EB，点D是AC的中点，

∴△ABE的面积≠△BCD的面积，

∴△ABF的面积和四边形DFEC的面积不相等，故②错误；

③过D点作DG∥BC，

∵点D是AC的中点，

∴DG=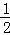EC，

∵EC=2EB，

∴DG=BE，

∵DG∥BC，

∴∠DGF=∠BEF，∠GDF=∠EBF，

在△DGF与△BEF中，

，

∴△DGF≌△BEF（ASA），

∴DF=BF，

∴点F是BD的中点，故③正确；

④四边形DFEC的面积=18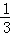﹣18×﹣18××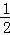

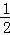
=18﹣6﹣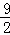

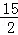=，故④正确．

故正确的结论有①③④．

故答案为：①③④．