
科目:初中数学 来源: 题型:解答题
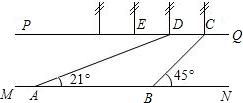 峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$).
峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了了解八年级学生的课外阅读情况,学习随机调查了该年级25名学生,得到了他们上周双休日课外阅读时间(记为t,单位:时)的一组数据样本,其扇形统计图如图所示.
为了了解八年级学生的课外阅读情况,学习随机调查了该年级25名学生,得到了他们上周双休日课外阅读时间(记为t,单位:时)的一组数据样本,其扇形统计图如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com