Question

10．已知平行四边形ABCD位置在平面直角坐标系中如图1所示，BC=AC，且OA=6，OC=8．
（1）求点D的坐标；
（2）动点P从点C出发，以每秒1个单位的速度沿线段以向终点A运动，动点Q从点A出发以每秒2个单位的速度沿4射线AD运动，两点同时出发，当P到达终点时，点Q停止运动，在运动过程中，过点Q作MQ∥AB交射线AC于M（如图2）．设PM=y，运动时间为t（t＞0），求y与t的函数关系式，并直接写出自变量的取值范围；
（3）在（（2）的条件下，作点P关于直线CD的对称点P′（如图3），当P′D=$\sqrt{37}$时，求运动时间t．

Answer 1

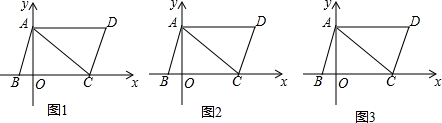
分析 （1）首先根据题意，判断出点A、C、E、B的坐标各是多少，然后根据点E是BD的中点，求出点D的坐标是多少即可．
（2）首先求出当P、M重合时，t=$\frac{10}{3}$；然后分两种情况：①当0$＜t＜\frac{10}{3}$时；②当$\frac{10}{3}$≤t≤10时；判断出y与t的函数关系式，并直接写出自变量的取值范围即可．
（3）首先连接PP′交CD于点F，连接PD，作AG⊥CD于点G，然后求出AB、CD、CG、AG、PF、CF的值各是多少；最后在Rt△PDF中，根据勾股定理，可得PD²=PF²+DF²，据此求出当P′D=$\sqrt{37}$时，运动时间t是多少即可．

解答 解：（1）如图1，连接BD交AC于点E，，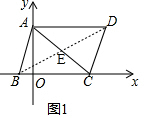
∵OA=6，OC=8，
∴点A的坐标是（0，6），点C的坐标是（8，0），
∴AC的中点E的坐标是（4，3），
在Rt△OAC中，
AC=$\sqrt{{OA}^{2}{+OC}^{2}}=\sqrt{{6}^{2}{+8}^{2}}=10$，
∵BC=AC，
∴BC=10，点B的坐标是（-2，0），
∵平行四边形ABCD中，点E也是BD的中点，
4×2-（-2）=10，3×2-0=6，
∴点D的坐标是（10，6）．

（2）∵BC=AC，BC=AD，
∴AC=AD，
又∵MQ∥AB，
∴AM=AQ=2t，
当P、M重合时，
2t+t=10，
解得t=$\frac{10}{3}$．
①如图2，，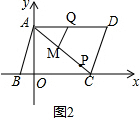
当0$＜t＜\frac{10}{3}$时，
y=10-2t-t=10-3t．

②如图3，，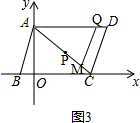
当$\frac{10}{3}$≤t≤10时，
y=AM+CP-AC=2t+t-10=3t-10．
综上，可得
y=$\left\{\begin{array}{l}{10-3t，0＜t＜\frac{10}{3}}\\{3t-10，\frac{10}{3}≤t≤10}\end{array}\right.$

（3）如图4，连接PP′交CD于点F，连接PD，作AG⊥CD于点G，，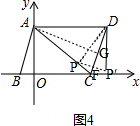
∵AB=$\sqrt{{OA}^{2}{+OB}^{2}}=\sqrt{{6}^{2}{+2}^{2}}=2\sqrt{10}$，
∴CD=2$\sqrt{10}$，CG=$\sqrt{10}$，
∴AG=$\sqrt{{AC}^{2}{-CG}^{2}}=\sqrt{{10}^{2}{-（\sqrt{10}）}^{2}}=3\sqrt{10}$，
∵点P与点P′关于CD对称，
∴PP′⊥CD，PD=P′D=$\sqrt{37}$，
又∵AG⊥CD，
∴PP′∥CD，
∴$\frac{CP}{AC}=\frac{PF}{AG}=\frac{CF}{CG}$，
即$\frac{t}{10}=\frac{PF}{3\sqrt{10}}=\frac{CF}{\sqrt{10}}$，
解得PF=$\frac{3\sqrt{10}}{10}t$，CF=$\frac{\sqrt{10}}{10}t$，
∴DF=CD-CF=2$\sqrt{10}$-$\frac{\sqrt{10}}{10}t$，
在Rt△PDF中，
PD²=PF²+DF²，
∴${（\sqrt{37}）}^{2}{=（\frac{3\sqrt{10}}{10}t）}^{2}$+${（2\sqrt{10}-\frac{\sqrt{10}}{10}t）}^{2}$，
整理，可得
t²-4t+3=0，
解得t=1或t=3，
即当P′D=$\sqrt{37}$时，运动时间t=1或t=3．

点评 （1）此题主要考查了四边形综合题，考查了分析推理能力，考查了分类讨论思想的应用，考查了数形结合思想的应用，要熟练掌握．
（2）此题还考查了平行四边形的性质和应用，以及直角三角形的性质和应用，以及勾股定理的应用，要熟练掌握．