
分析 (1)将点M(2,1)代入二次函数y=ax2-2bx+1可得结果;
(2)首先根据a与b的关系得出对称轴,然后根据对称性,解得A、B的坐标,设二次函数解析式为交点式y=a(x-$\frac{1}{2}$)(x$-\frac{3}{2}$),将M坐标代入解得a,将a代入求得表达式;
(3)分别把A(m,y1),B(m+2,y2)两点代入y=$\frac{4}{3}$x2-$\frac{8}{3}$x+1,得到y2-y1=($\frac{4}{3}$m2+$\frac{8}{3}$m+1)-($\frac{4}{3}$m2-$\frac{8}{3}$m+1)=$\frac{16}{3}m$,然后讨论:当$\frac{16}{3}$m<0;$\frac{16}{3}m$=0;$\frac{16}{3}m$<0即可.
解答 解:(1)将点M(2,1)代入二次函数y=ax2-2bx+1得,
1=a×22-2×2×b+1,
解得:b=a.
故答案为:a;
(2)∵b=a,
∴二次函数y=ax2-2bx+1的对称轴为:x=-$\frac{-2b}{2a}$=1,
∵二次函数的图象与x轴的两个交点为A、B,AB=1,
设点A在点B的左侧,
∴点A的横坐标xA=1-$\frac{1}{2}$=$\frac{1}{2}$,点B的横坐标xB=1+$\frac{1}{2}$=$\frac{3}{2}$,
∴设二次函数的表达式为:y=a(x-$\frac{1}{2}$)(x$-\frac{3}{2}$),
把点M(2,1)代入得:1=a(2-$\frac{1}{2}$)(2$-\frac{3}{2}$),解得:a=$\frac{4}{3}$,
∴二次函数的表达式为:y=$\frac{4}{3}$(x-$\frac{1}{2}$)(x$-\frac{3}{2}$),整理得y=$\frac{4}{3}$x2-$\frac{8}{3}$x+1;
(3)∵A(m,y1),B(m+2,y2)两点都在y=$\frac{4}{3}$x2-$\frac{8}{3}$x+1函数的图象上,
∴y1=$\frac{4}{3}$m2-$\frac{8}{3}$m+1;,y2=$\frac{4}{3}$(m+2)2-$\frac{8}{3}$(m+2)+1=$\frac{4}{3}$m2+$\frac{8}{3}$m+1,
∴y2-y1=($\frac{4}{3}$m2+$\frac{8}{3}$m+1)-($\frac{4}{3}$m2-$\frac{8}{3}$m+1)=$\frac{16}{3}m$,
当$\frac{16}{3}$m<0,即m<0时,y1>y2;
当$\frac{16}{3}$m=0,即m=0时,y1=y2;
当$\frac{16}{3}$m>0,即m>0时,y1<y2.
点评 本题考查了用待定系数法求二次函数的解析式、二函数的性质,掌握抛物线与x轴的两个交点关于对称轴对称,利用分类讨论是解答此题的关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
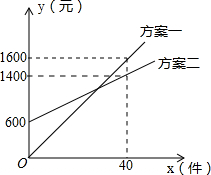 某销售公司推销一种产品,设x(种)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:
某销售公司推销一种产品,设x(种)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
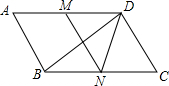 如图,在?ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD
如图,在?ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
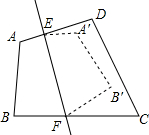 如图,四边形ABCD沿直线EF对着,点A、B的对应点A′,B′落在四边形内部,若∠C+∠D=160°,则∠DEA′+∠CFB′的度数是40°.
如图,四边形ABCD沿直线EF对着,点A、B的对应点A′,B′落在四边形内部,若∠C+∠D=160°,则∠DEA′+∠CFB′的度数是40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com