
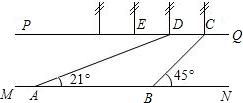
 峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$).
峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$). 分析 设河的宽度为d米,过D作DF⊥MN于F,过C作CH⊥MN于G,构建直角三角形:Rt△ADF、Rt△BCG.通过解这两个直角三角形分别求得AF的值,依次列出关于d的方程,通过解方程来求d的值即可.
解答 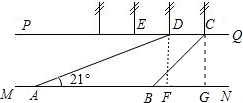 解:设河的宽度为d米,
解:设河的宽度为d米,
过D作DF⊥MN于F,过C作CH⊥MN于G,
在Rt△ADF中,$tan21°=\frac{DF}{AF}=\frac{d}{AF}$,
∴$AF=\frac{d}{tan21°}$,
在Rt△BCG中,$tan45°=\frac{CG}{BG}=\frac{d}{BG}$,即BG=d,
又∵AB=175,$tan21°≈\frac{3}{8}$,两树的间隔为50米,
∴AF=AG-50=AB+BG-50,
∴$\frac{8}{3}$d=175+d-50,
解得:d=75.
答:峨眉河的宽度约为75米.
点评 本题考查了解直角三角形的应用.当题中给出一定的度数时,要充分利用这些度数构造相应的直角三角形,利用锐角三角函数知识求解.


科目:初中数学 来源: 题型:填空题
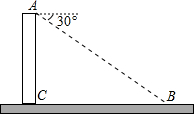 如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为10$\sqrt{3}$m(结果保留根号).
如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为10$\sqrt{3}$m(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
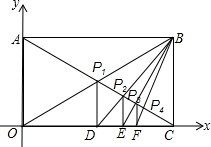 平面直角坐标系中,矩形OABC的顶点A,C分别在坐标轴上,顶点B在第一象限内,如图所示,且OA=a,OC=b.请根据下列操作,完成后面的问题.
平面直角坐标系中,矩形OABC的顶点A,C分别在坐标轴上,顶点B在第一象限内,如图所示,且OA=a,OC=b.请根据下列操作,完成后面的问题.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
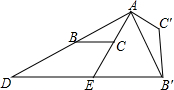 如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$.
如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
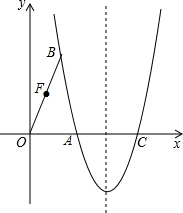 如图,在平面直角坐标系中,抛物线y=$\frac{8\sqrt{2}}{5}$x2+bx+c经过点A($\frac{3}{2}$,0)和点B(1,2$\sqrt{2}$),与x轴的另一个交点为C.
如图,在平面直角坐标系中,抛物线y=$\frac{8\sqrt{2}}{5}$x2+bx+c经过点A($\frac{3}{2}$,0)和点B(1,2$\sqrt{2}$),与x轴的另一个交点为C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
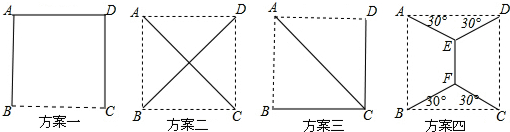
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com